1) решите уравнение 3cos^2x+sinxcosx=0 2) даны векторы a{2;4;0}, b{1;1;-3}. Найдите длину вектора d=a+5b

Question

Математика: 1) решите уравнение 3cos^2x+sinxcosx=0 2) даны векторы a{2;4;0}, b{1;1;-3}. Найдите длину вектора d=a+5b

Рудиковичный · Answer

1) решите уравнение 3cos^2x+sinxcosx=0

Поделим все уравнение на cos^2x cos^2x≠0

3+tgx=0

tgx=-3

x=arctg(-3)+πk, k∈Z

x=-arctg3+πk, k∈Z

2) даны векторы a{2;4;0}, b{1;1;-3}. Найдите длину вектора d=a+5b

5b(5;5;-15)

d=a+5b(2+5;4+5;0+(-15))

d=a+5b(7;9;-15)

Длинна вектора d=a+5b=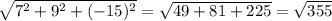 $\sqrt{7^2+9^2+(-15)^2 }=\sqrt{49+81+225} =\sqrt{355$

Пошаговое объяснение:

$1) решите уравнение 3cos^2x+sinxcosx=0 2) даны векторы a{2;4;0}, b{1;1;-3}. Найдите длину вектора d=$