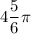1) решите уравнение: (2sin^2x-7sinx+3)*log по основанию 2 (x-8)=0 2)найдите все корни уравнения, принадлежащие данному промежутку (3пи; 6пи)
Другие вопросы по теме Математика
Популярные вопросы
- Обороты there is there are (+, -, ? ) - письменно...
3 - Если андреев даст петрову 300р, то денег у нтх станет поровну....
3 - Придумайте и запишите четыре числовых выражения и четыре буквенные...
1 - Стриж,печ,рож,шалаш,нож,мяч,дрож,тиш,корж,клич фальш,ткач,,фарш,дич,экипаж,брош,плач,полноч,мышь....
2 - Вдень рождения винни- пуху подарили бочонок с мёдом массой 9 кг....
2 - Решите .8класс 22р в четвёртой степени q во второй степ 99 р в...
2 - Решить . во время эскурсии дорога из школы в парк и обратно заняла...
3 - Скакой скоростью надо бросить шарик вниз с высоты 3 метра чтобы...
2 - Умихаила в 2 раза больше орехов чем у николая ,а у пети в 3 раза...
3 - Вставить глаголы в правильной i (do) my final year at school and...
3
I. (2sin²x - 7sinx + 3) · log₂ (x-8) = 0
ОДЗ : x-8 > 0; x > 8
Произведение равно нулю, когда один из множителей равен нулю.
1) 2sin²x - 7sinx + 3 = 0 - квадратное уравнение с неизвестным sinx
D = 7² - 4·2·3 = 25 = 5²
sin x = (7+5)/4 = 3 - не подходит под условие |sin x| ≤ 1
sin x = (7-5)/4 = 1/2
x₁ = π/6 + 2πn, n∈N, n≥2 ( ОДЗ: π/6 + 4π ≈ 13,1 > 8)
x₂ = 5π/6 + 2πk, k∈N ( ОДЗ: 5π/6 + 2π ≈ 8,9 > 8)
2) log₂ (x-8) = 0 ⇒ x - 8 = 2⁰
x = 1 + 8; x₃ = 9
==========================
II. x ∈ (3π; 6π)
3) x₃ = 9 < 9,4 ≈ 3π - не входит в интервал
ответ: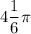 ;
;