1) решите уравнение: 2 cos(x-π/6)+√2=0 на промежутке 0°<x<2π 2) решите уравнение: 2cos²x-3sinx=0

Ответы

21Oleg12 26.12.2021 15:30

Пошаговое объяснение:

$2cos(x-\dfrac{\pi }{6} )+\sqrt{2} =0;\\\\2cos(x-\dfrac{\pi }{6} )=-\sqrt{2};\\\\cos(x-\dfrac{\pi }{6} )=-\dfrac{\sqrt{2} }{2} ;\\\\x-\dfrac{\pi }{6}=\pm \dfrac{3\pi }{4} +2\pi n,~n\in\mathbb {Z};\\\\$

$\left[\begin{array}{l} x-\dfrac{\pi }{6}= - \dfrac{3\pi }{4} +2\pi k,~k\in\mathbb {Z} \\\\ x-\dfrac{\pi }{6} = \dfrac{3\pi }{4} +2\pi n,~n\in\mathbb {Z} \end{array} \right.\Leftrightarrow \left[\begin{array}{l} x=\dfrac{\pi }{6} - \dfrac{3\pi }{4} +2\pi k,~k\in\mathbb {Z} \\\\ x=\dfrac{\pi }{6} + \dfrac{3\pi }{4} +2\pi n,~n\in\mathbb {Z} \end{array} \right.\Leftrightarrow$

$\Leftrightarrow \left[\begin{array}{l} x=\dfrac{\pi }{6}^{\backslash4} - \dfrac{3\pi }{4}^{\backslash3} +2\pi k,~k\in\mathbb {Z} \\\\ x=\dfrac{\pi }{6}^{\backslash4} + \dfrac{3\pi }{4}^{\backslash3} +2\pi n,~n\in\mathbb {Z} \end{array} \right.\Leftrightarrow\left[\begin{array}{l} x= - \dfrac{5\pi }{12} +2\pi k,~k\in\mathbb {Z} \\\\ x= \dfrac{5\pi }{4} +2\pi n,~n\in\mathbb {Z} \end{array} \right.$

Найдем корни, принадлежащие промежутку

$k=1,x= -\dfrac{5\pi }{12} +2\pi= \dfrac{-5\pi +24\pi }{12} =\dfrac{19\pi }{24}$

$n=0,x= \dfrac{5\pi }{4}$

ответ: $\dfrac{5\pi }{4} ;\dfrac{19\pi }{24} .$

$2cos^{2} x-3sinx=0;\\2(1-sin^{2} x)-3sinx=0 ;\\2-2sin^{2} x-3sinx=0|\cdot(-1);\\2sin^{2} x+3sinx-2=0$

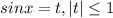Пусть $sinx=t, |t|\leq 1$ . Тогда уравнение принимает вид

$2t^{2} +3t-2=0;\\D= 3^{2} -4\cdot2\cdot(-2)=9+16=25=5^{2} \\ \left [\begin{array}{l} t= \dfrac{-3-5}{4} , \\\\ t= \dfrac{-3+5}{4}; \end{array} \right.\Leftrightarrow \left [\begin{array}{l} t= -2 , \\\\ t= \dfrac{1}{2}. \end{array} \right.$

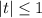Условию $|t|\leq 1$ удовлетворяет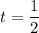 $t= \dfrac{1}{2}$

Тогда

$sinx=\dfrac{1}{2} ;\\\\ \left[\begin{array}{l}x = \dfrac{\pi }{6} +2\pi k,~k\in\mathbb {Z}, \\\\ x = \dfrac{5\pi }{6} +2\pi n,~n\in\mathbb {Z} \end{array} \right.$