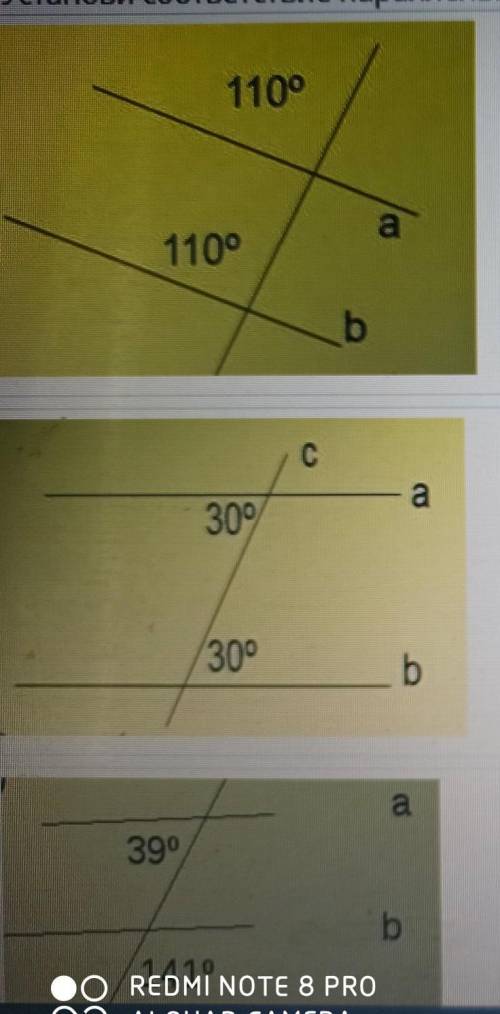
1)Прямые а и б параллельны,так как накрест лежащие углы равны. 2)прямые а и б параллельны,так как сумма внутренних односторонних углов равна 180°
3)прямые а и б параллельны,так как соответственные углы равны.
какие картинки подайдут к этому​

Добрый день!

Представьте, что у нас есть две прямые линии, назовем их а и б. Мы хотим определить, являются ли эти прямые параллельными или нет.

Есть несколько способов выяснить это. В данном вопросе предлагается рассмотреть три возможных причины, по которым прямые a и b могут быть параллельными. Давайте разберем каждую из них в отдельности и посмотрим, как они применяются к данным линиям.

1) Первая причина, которую нам дается, - это то, что накрест лежащие углы равны. Чтобы было проще представить себе, что такое накрест лежащие углы, посмотрите на картинку, представленную выше. На картинке видно, что есть две пересекающиеся прямые линии и четыре угла, образованных этим пересечением. Накрест лежащие углы - это углы, которые находятся напротив друг друга, но при этом находятся по разные стороны пересекающейся линии. Например, угол 1 будет накрест лежащим для угла 4, и угол 2 будет накрест лежащим для угла 3. Если накрест лежащие углы равны, это означает, что мы можем сказать, что прямые линии параллельны.

2) Вторая причина, которую нам дается, - это то, что сумма внутренних односторонних углов равна 180°. Чтобы понять, что такое односторонние углы, представьте, что вы берете линейку и закрываете ей одну из сторон угла. Внутри каждого угла останется только одна сторона, и это называется односторонним углом. На картинке выше уголы 1 и 4 являются односторонними для линии а, а уголы 2 и 3 - для линии б. Если сумма внутренних односторонних углов равна 180°, то это означает, что прямые линии параллельны.

3) Третья причина, которую нам дается, - это то, что соответственные углы равны. Соответственные углы - это углы, которые находятся по разные стороны пересекающейся линии, но находятся на одинаковой стороне параллельных линий. Например, угол 1 будет соответственным углом для угла 2, и угол 4 будет соответственным углом для угла 3. Если соответственные углы равны, это означает, что прямые линии параллельны.

Итак, чтобы определить, являются ли прямые линии а и б параллельными или нет, мы можем рассмотреть каждую из этих трех причин. Если хотя бы одна из них верна, то мы можем сказать, что прямые линии параллельны.

В данной ситуации, посмотрев на картинку, мы видим, что накрест лежащие углы и соответственные углы равны, что означает, что две прямые линии а и б параллельны.