1. При каких значе каких значениях m верно равенство:
2 | m | + m = - m ?
Решите
Другие вопросы по теме Математика
Популярные вопросы
- Выпиши главное слово из словосочетания, какой частью речи оно является? 1....
3 - Узкая лента. просклонять словочетание...
2 - Начертите координатный луч, приняв, что единичный отрезок равен 2 см. отметьте...
2 - Написать сочинение па бел .лит браты-артысты...
1 - Выполните действия а) (1-j) - (7-3j) - (2+j) + (16-2j)...
1 - Какие книги ты любишь читать? почему? что тебя в них ? составь и напиши текст...
3 - Что описывается в рассказе каштанка...
1 - Язык 7 класс , не хочу получить 1)people will/won t drive solar cars in 2050...
3 - Какие проблемы общества затрагиваются в рассказе старый гений н. с. лескова?...
2 - An orchestra can t play without: (conductor,barrister,controller,inspector)...
1
ответ: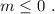
Если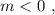 то
то 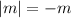 , тогда уравнение можно переписать в виде
, тогда уравнение можно переписать в виде
Если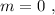 то
то 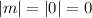 , и уравнение можно переписать в виде
, и уравнение можно переписать в виде
Если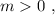 то
то 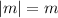 , и уравнение можно переписать в виде
, и уравнение можно переписать в виде
ответ: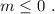
ответ: При всех m≤0
Пошаговое объяснение:
2|m| +m = -m⇒ 2|m| = -2m⇒ |m| = -m
Тут можно сделать вывод что m = 0 и ошибиться, поясню:
Раскроем модуль:
1) m ≥ 0
m = -m⇒ 2m = 0 ⇒ m =0
2) m< 0
-m = -m ⇒m =m
Из пункта 1 и 2 видно, что равенство верно при всех не положительных значениях m.