1) по координатам точек а, в, с для указанных векторов найти: (а) модуль вектора а (б) скалярное произведение векторов а, b (в) проекцию вектора с на вектор d (г) координаты точки м, делящей отрезок перпендикулярно в отношении α/β а(-2; -3; -4), в(2; -4; 0), с(1; 4; 5), вектор а= 4 вектор ас-8 вектор вс,вектор b=вектор с= вектор ас, вектор d= вектор вс, i=ав,α= 4,β=2 2)вычислить производные: а) у= √18-√6х б) у= 7- 9х^2- 13х- 4х^3 в) у= (х^2-1)^3
Другие вопросы по теме Математика
Популярные вопросы
- 104 и 105 и лучший ответ дано решение и ответ...
3 - B) Put the words in the correct order to form questions based on the text....
2 - Какой объём кислорода потребуется для сжигания 40 л смеси метана с этаном,...
3 - Напишите письмо барыне из рассказа «Муму». Выскажите все, что вы думаете...
2 - Четные числа : 0,2,4,6,8 - если последняя цифра номера телефона заканчивается...
3 - 6 сынып тест қазақ тілі есімдік тақырыбына арналған кестелі тест тапсырмасы...
3 - Найди сумму координат точек A, B, C и D. ответ запиши в виде десятичной...
1 - Скласти з двох речень одне з дієприкметникові зворотом, записати. 1)Невеличкі...
3 - 3. Составь истинные и ложные высказывания (до 2 каждог Приближённое значениео)...
3 - В равнобедренном треугольнике угол при вершине, противолежащей основанию...
2
1) a) |a|=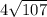
б) (a,b)=-228
в) Проекция вектора c на вектор d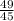
г) Координаты точки М, делящей отрезок AB в отношении α/β = 4/2:
2) а)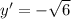
б) y'=-18·x-13-12·x²
в) y'=6·x·(x²-1)²
Пошаговое объяснение:
Векторы выделены жирным шрифтом!
Если p=(x1; y1; z1), то длина вектора p:
|p|=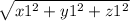
Если p=(x1; y1; z1) и q=(x2; y2; z2), то скалярное произведение векторов p и q: (p,q)=x1·x2+y1·y2+z1·z2
Проекция вектора b на вектор a : прₐb=(a,b)/|a|
Координаты точки M, делящей отрезок AB в заданном отношении λ определяются по формулам
1) А(-2; -3; -4), В(2; -4; 0), С(1; 4; 5)
AB=B-A=(2; -4; 0)-(-2; -3; -4)=(2-(-2); -4-(-3); 0-(-4))=(4; -1; 4)
b=c=AC=C-A=(1; 4; 5)-(-2; -3; -4)=(1-(-2); 4-(-3); 5-(-4))=(3; 7; 9)
d=BC=C-B=(1; 4; 5)-(2; -4; 0)=(1-2; 4-(-4); 5-0)=(-1; 8; 5)
а) a=4·AC-8·BC=4·(3; 7; 9)-8·(-1; 8; 5)=(12; 28; 36)-(-8; 64; 40)=
=(12-(-8); 28-64; 36-40)=(20; -36; -4)
|a|=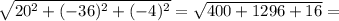
б) (a,b)=20·3+(-36)·7+(-4)·9=60-252-36= -228
в) Проекция вектора c на вектор d :
г) Координаты точки М, делящей отрезок AB в отношении α/β = 4/2:
А(-2; -3; -4), В(2; -4; 0)
2) Производные функции:
а)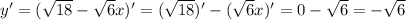
б) y'=(7-9x²-13x-4x³)'=(7)'-(9x²)'-(13x)'-(4x³)'=0-9·2·x-13·1-4·3·x²=-18·x-13-12·x²
в) y'=((x²-1)³)'=3·(x²-1)²·(x²-1)'=3·(x²-1)²·2·x=6·x·(x²-1)²