1)обчислити: 2arcsin(-1)-4arcctg(-1); 2)розв'язати нерівність: ctgx> -1; 3)розв'язати рівняння: 5cos^2x-6cosx=0; 4)довести тотожність: tg(arcsin1/2+arccos0)=-√3; 5)розв'язати рівняння: sinx+sin3x/cosx=0; 6)знайти розв'язки нерівності: tg(4x+π/4)+1≤0; 7)розв'язати систему рівнянь: 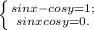
Другие вопросы по теме Математика
Популярные вопросы
- Язык относится к числу мировых языков. достоинства: 1 огромный...
2 - Распространяйте предложения второстепенными членами...
2 - Определить падеж имен существительных собирают сок...
3 - Почему автор отказался от деления текста на строфы в стихотворении...
1 - От какого события мусульмани начинают отсчёт своего (літочислення)(не...
2 - Сколько страниц в книге каролина нил гейман...
3 - Основные устройства компьютера?...
3 - Какие из перечисленных плоскостей составляют пространственный...
1 - Всосуде, теплоёмкость которого равна 188 дж/°с, находится 2 л...
1 - 20 в статье 39 великой хартии вольностей говорится: ни один свободный...
3
1) 2arcsin(-1)-4arcctg(-1) = -2π/2-4(π - arcctg1) = -π - 4(π - π/4) = -π - 4(3π/4) = -π - 3π = -4π.
2) ctgx>-1; πn < x < 3π/4 + πn, n∈Z.
3) 5cos^2x-6cosx=0; cosx(5cosx-6)=0;
cosx = 0 або 5cosx-6 = 0.
x = π/2 + πn, n∈Z. cosx = 1,2 - немає розв'язків.
Відповідь: π/2 + πn, n∈Z.
4) tg(arcsin1/2+arccos0) = -√3.
tg(arcsin1/2+arccos0) = tg(π/6+π/2) = -сtg(π/6) = -√3, що й треба було довести.
5) sinx+sin3x/cosx=0. ОДЗ: cosx ≠ 0.
sinx+sin3x = 0; 2sin2xcosx = 0;
sinx = 0 або cosx = 0 - не задовольняє ОДЗ.
x = πn, n∈Z.
6) tg(4x+π/4)+1 ≤ 0; tg(4x+π/4) ≤ -1; -π/2 + πn ≤ 4x+π/4 ≤ -π/4 + πn;
-π/2- π/4 + πn ≤ 4x ≤ -π/4 - π/4 + πn, n∈Z; -3π/4 + πn ≤ 4x ≤ -π/2 + πn, n∈Z;
-3π/8 + πn/4 ≤ x ≤ -π/8 + πn/4, n∈Z.
7) Розв'язати систему рівнянь: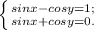 Додамо перше і друге рівняння системи:
Додамо перше і друге рівняння системи: 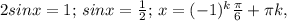 k∈Z.
k∈Z.
Віднімемо друге і перше рівняння системи:
Відповідь: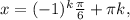 k∈Z;
k∈Z; 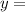 ±
±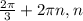 ∈Z.
∈Z.