1. Математика
  2. 1. найти область определение

1. найти область определение функции
z= \frac{1}{\sqrt{x^{2}+y^{2}-5 }}
2. вычислить значение производной сложной функции
u=\frac{x}{y} где x=e^{t}, y=2-e^{2t} при t = 0

victorov113 victorov113    1   29.08.2019 11:45    0

Ответы
NadiaU0 NadiaU0  06.10.2020 02:49

Пошаговое объяснение:

1)\; \; z=\frac{1}{\sqrt{x^2+y^2-5}}\\\\OOF:\; \; x^2+y^2-50\; \; \to \; \; x^2+y^25\; ,\; \; \; x^2+y^2(\sqrt5)^2

Обл. определения ф-ции является часть плоскости, которая находится вне круга с центром в точке  (0,0) и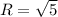  R=\sqrt5  .

P.S.  Граница круга ( окружность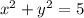  x^2+y^2=5  )  в ООФ не входит .

2)\; \; U=\frac{x}{y}\; \; ,\; \; x=e^{t}\; \; ,\; \; y=2-e^{2t}\\\\\frac{dU}{dt}=\frac{\partial U}{x}\cdot \frac{dx}{t}+\frac{\partial U}{\partial y}\cdot \frac{dy}{dt}\\\\\frac{dU}{dt}=\frac{1}{y}\cdot e^{t}-\frac{x}{y^2}\cdot (-2e^{2t})=\frac{e^{t}}{y}\cdot (1+\frac{2xe^{t}}{y})\\\\\frac{dU}{dt}\Big |_{t=0}=\Big (\frac{e^{t}}{2-e^{2t}}\cdot (1+\frac{2e^{t}\cdot e^{t}}{2-e^{2t}})\Big )\Big |_{t=0}=\frac{1}{2-1}\cdot (1+\frac{2}{2-1})=1+2=3


1. найти область определение функции z= <img src= 2. вычислить зна" />
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Изачка Изачка  25.08.2019 12:00
Водну столовую 5 одинаковых ящиков фруктов,в другую -2 таких же ящика.в первую столовую на 24 кг фруктов больше, чем во вторую.сколько килограммов фруктов в каждую...
masha091115 masha091115  25.08.2019 12:00
Собственная скорость теплохода 53,2 км ч скорость теплохода против течения 50,5 км ч . найдите скорость теплохлда по течению рек...
timcherkasov07p02k8v timcherkasov07p02k8v  25.08.2019 12:00
(8050*408-278400)/900 решить по действиям...
2007AZAZA 2007AZAZA  25.08.2019 12:00
Исследовать на выпуклость вогнутость перегиб у=x^4+4x^3+4x^2...
olmilevskaya1 olmilevskaya1  25.08.2019 12:00
Как решения модули решать ,если складывать два отрицательных числа то получиться положительное...
PolinaSukova2 PolinaSukova2  25.08.2019 12:00
Решить 2 10 , 1 : на корабле с конфетами надпись 0,8 кг. 280 тг. какова цена 1 кг этих конфет . 2 : на пакете с мукой надпись 1,5 кг. 105 тг. какова цена 1 кг муки....
ЛёняЛАпочка ЛёняЛАпочка  25.08.2019 12:00
3класс,10номер заполни пропуски такими числами,чтобы получились верные записи. 1)14: 3=_( 2)42: 9=_( 3)53: 6=_( 4)36: 7=_( 5)27: 5=_( 6)68: 8=_( не ответы! решить...
t4dhjnd1u24ytgh t4dhjnd1u24ytgh  25.08.2019 12:00
Первая машина может самостоятельно очистить улицу за 5 часов, а вторая за 10 часов. обе машины одновременно начали очищать улицу. пророботав 1 час 48 мин первая...
arsigonin arsigonin  25.08.2019 12:00
Выполните умножение 44 1)6,3*1,84 2)5,6*2,5 3)0,8*4,6 4)0,3*1,5 5)1,9*3,5 6)0,2*8,5 7)2,5*0,9 8)1,7*0,3...
lydakkr lydakkr  25.08.2019 12:00
2(8a +7b) + 4(a-2b) выражение 7 минут до урока...

Популярные вопросы