1) Найти объем правильной усеченной пирамиды, в основании которой квадраты со сторонами 4 и 9 см, а высота пирамиды равна 6.

2) Найдите объем усеченной пирамиды, основание которой прямоугольные треугольники. Катеты большего основания равны 27 и 36 см. Стороны меньшего основания в 3 раза меньше, а высота пирамиды равна 30 см.

Ответы

asd000fgh000 14.10.2020 17:03

Пошаговое объяснение:

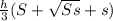
V= $\frac{h}{3} (S+\sqrt{Ss} +s)$

S=9^2=81

s=4^2=16

V=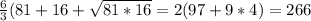 $\frac{6}{3} (81+16+\sqrt{81*16} =2(97+9*4)=266$

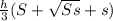
V= $\frac{h}{3} (S+\sqrt{Ss} +s)$

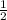S= $\frac{1}{2}$ *27*36=486

s=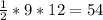 $\frac{1}{2} *9*12=54$

V=10(486+54+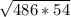 $\sqrt{486*54}$ )=5400+10*9*3*6=7020

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

Бата194 16.03.2021 10:05

Найти матрицу (1 0 3. 2 -1 0. 3 2 7)...

Anonim307 16.03.2021 10:05

ShadowFlcus 16.03.2021 10:05

Fosa1 16.03.2021 10:07

paris555 16.03.2021 10:07

plagiatik6 16.03.2021 10:07

grimangus 20.07.2019 08:10

Заранее ! решите самым легким...

lariliv75 20.07.2019 08:10

даша34430 20.07.2019 08:10

MedinaIsk 20.07.2019 08:10