1) Найти центр, оси, вершины, фокусы, эксцентриситет и асимптоты гиперболы, если её уравнение 16x^2-9y^2-64x-54y-161=0
2) Найти вершину, фокус, ось и директрису параболы, если ее уравнение y^2+2y+4x-11=0
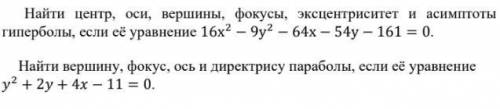
Другие вопросы по теме Математика
Популярные вопросы
- Які з варіантів відповідей рівняння дисоціації речовини записані...
3 - Представление рационального числа в виде бесконечной десятичной...
1 - Основные положение конвенции, устанавливающий единообразный закон...
1 - Нужно поставить глаголы в нужную форму...
3 - в двумя вопросами. 1) Если необходимо найти путь за 7-ю секунду...
3 - Все ли многолетние растения, произрастающие на нашей пла- нете,...
2 - Написать уравнение прямой l, удовлетворяющей условию. Сделать рисунок,...
2 - МӘТІНМЕН Жua ТЫҢДАЛЫМ АЙТЫЛЫМ5-тапсырма. Өлеңді тыңда. Өзіңнің...
3 - КАЗАХСКИЙ НАДО НЕ НАДО СПАМИТЬ ОТВЕТЬТЕ Автор шығармасын неге «Жантаза»...
2 - Какое расстояние проедет автомобиль за 7/16ч, если его скорость...
3
(x-h)^2/a^2 - (y-k)^2/b^2 = 1,
где (h,k) - координаты центра гиперболы.
Для этого приведем уравнение гиперболы в стандартную форму:
16x^2 - 9y^2 - 64x - 54y - 161 = 0.
Перегруппируем члены:
16x^2 - 64x - 9y^2 - 54y = 161.
Раскроем скобки:
16(x^2 - 4x) - 9(y^2 + 6y) = 161.
Для завершения квадратов вычислим дополнительные члены и добавим их в уравнение:
16(x^2 - 4x + 4) - 9(y^2 + 6y + 9) = 161 + 16*4 - 9*9.
Упростим:
16(x - 2)^2 - 9(y + 3)^2 = 144.
Разделим обе части уравнения на 144, чтобы привести к стандартному виду:
(x - 2)^2/9 - (y + 3)^2/16 = 1.
Теперь у нас есть уравнение гиперболы в стандартной форме. Мы видим, что a^2 = 9 и b^2 = 16. Следовательно, a = 3 и b = 4.
Теперь можем найти оси гиперболы. Они представляют собой отрезки, проходящие через центр и ортогональные друг другу. В данном случае, оси гиперболы параллельны осям координат.
Ось x проходит через центр гиперболы, поэтому ее уравнение имеет вид x = h, где h - координата центра, равная 2.
Ось y проходит через центр гиперболы, поэтому ее уравнение имеет вид y = k, где k - координата центра, равная -3.
Теперь найдем вершины гиперболы. Вершины находятся на оси x и отстоят от центра на расстояние a (в данном случае a = 3).
Так как центр находится в точке (2, -3), вершины будут иметь координаты (2 +/- a, -3).
Таким образом, первая вершина имеет координаты (2 + 3, -3) = (5, -3), а вторая вершина имеет координаты (2 - 3, -3) = (-1, -3).
Фокусы гиперболы можно найти с использованием формулы: c^2 = a^2 + b^2, где c - расстояние от центра до фокуса.
В данном случае a = 3 и b = 4. Подставим значения:
c^2 = 3^2 + 4^2 = 9 + 16 = 25.
c = sqrt(25) = 5.
Так как фокусы гиперболы находятся на оси x, с координатами (h +/- c, k), в данном случае координаты фокусов будут (2 +/- 5, -3).
Первый фокус имеет координаты (2 + 5, -3) = (7, -3), а второй фокус имеет координаты (2 - 5, -3) = (-3, -3).
Эксцентриситет гиперболы вычисляется по формуле: e = c/a.
В нашем случае e = 5/3.
Асимптоты гиперболы можно найти по формуле: y = +/- (b/a)x + k, где k - координата центра гиперболы.
В данном случае, асимптоты имеют уравнения:
y = +/- (4/3)x - 3.
2) Для начала приведем уравнение параболы к стандартному виду:
y^2 + 2y + 4x - 11 = 0.
Перегруппируем члены:
y^2 + 2y = -4x + 11.
Для завершения квадрата (y + 1)^2 в левой части уравнения, добавим и вычтем 1:
y^2 + 2y + 1 - 1 = -4x + 11.
(y + 1)^2 - 1 = -4x + 11.
(y + 1)^2 = -4x + 12.
Теперь уравнение параболы имеет вид (y + 1)^2 = -4(x - 3). Мы видим, что вершина параболы находится в точке (3, -1).
Так как коэффициент перед x отрицательный, ось параболы будет вертикальной и проходит через вершину параболы.
Теперь найдем фокус параболы. Он находится по формуле (h, k + 1/(4a)), где (h, k) это координаты вершины параболы, а а - коэффициент при x в уравнении параболы.
В данном случае (h, k) = (3, -1) и a = -1/4.
Теперь можем вычислить фокус:
f = (3, -1 + 1/(4*(-1/4))) = (3, -1 - 4) = (3, -5).
Ось параболы проходит через вершину и параллельна оси x в данном случае.
Это означает, что ее уравнение имеет вид y = k, где k - координата вершины параболы, равная -1.
Директриса параболы находится на расстоянии a (в данном случае a = -1/4) от вершины и параллельна оси x.
Для вычисления директрисы добавим и вычтем a в координате вершины параболы:
d = (3, -1 - (-1/4)) = (3, -3/4).
Таким образом, директриса параболы имеет уравнение x = 3.