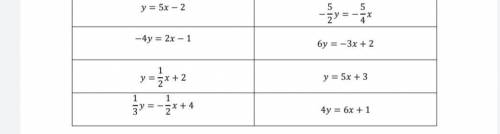
1) Напишите условие параллельных прямых .2)Найдите параллельную линию от столбца 2 к строкам в столбце 1 (если есть)! 1-й столбец 2-й столбец.
Другие вопросы по теме Математика
Популярные вопросы
- Сравнение афин и спарты напишите вопросы и ответы!...
1 - Обозначьте члены предложения( подлежащее, сказуемое, дополнение, определение,...
1 - Как я отнашусь к реформама петра | отрицательно или положительно и доказать...
2 - Разложите числа 4104 и 5544 на простые множители...
3 - Только ли в школе приходиться учиться?...
2 - Почему в предложении равенство в любви и дружбе- вещь святая ставится тире...
1 - Что такое пятиборье в древней греции...
1 - Описать рабочий механизм какого нибудь траспорта и принцеп работы...
2 - Переведите қазақстан республикасының 1920-1925 жылдар аралығында ең алғашқы...
2 - 2-3 предложения о произведении лапти...
2
В решении.
Пошаговое объяснение:
Сначала нужно преобразовать уравнения для наглядности.
1 столбик:
а) у = 5х - 2 без изменений;
б) -4у = 2х - 1
у = (2х - 1)/-4
у = -0,5х + 0,25;
в) у = 1/2 х + 2
у = 0,5х + 2;
г) 1/3 у = - 1/2 х + 4
у/3 = -х/2 + 4
Умножить уравнение (все части) на 6, чтобы избавиться от дробного выражения:
2у = -3х + 24
у = (-3х + 24)/2
у = -1,5х + 12.
2 столбик:
а) -5/2 у = -5/4 х
-5у/2 = -5х/4
Умножить уравнение (все части) на 4, чтобы избавиться от дробного выражения:
-10у = -5х
у = -5х/-10
у = 0,5х;
б) 6у = -3х + 2
у = (-3х + 2)/6
у = -0,5х + 1/3;
в) у = 5х + 3 без изменений;
г) 4у = 6х + 1
у = (6х + 1)/4
у = 1,5х + 0,25.
Условие параллельности прямых: k₁ = k₂; b₁ ≠ b₂.
Применить условие параллельности к уравнениям:
а) у = 5х - 2 в) у = 5х + 3;
б) у = -0,5х + 0,25 б) у = -0,5х + 1/3;
в) у = 0,5х + 2 а) у = 0,5х;