1. Математика
  2. 1+log2(x-2) log2(x^2-3x+2)Otvet

1+log2(x-2)>log2(x^2-3x+2)
Otvet'te pzh​

ppetrovaa ppetrovaa    3   29.03.2021 21:13    1

Ответы
HollywooD2016 HollywooD2016  28.04.2021 21:18

1+\log_2(x-2)\log_2[(x-2)(x-1)]

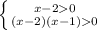
ОДЗ: \left \{ {{x-20} \atop {(x-2)(x-1)0}} \right.

Поскольку из первого неравенства следует, что x>2, делаем вывод, что не только x-2>0, но и x-1>0, а тогда и (x-1)(x-2)>0. Окончательно,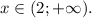 x\in(2;+\infty).

Поскольку логарифм произведения положительных чисел равен сумме логарифмов от сомножителей, можем исходное неравенство записать в виде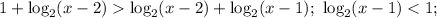 1+\log_2(x-2)\log_2(x-2)+\log_2(x-1);\ \log_2(x-1)

\log_2(x-1)

Пересекая с ОДЗ, получаем

ответ: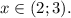 x\in(2;3).

Замечание. Отбрасывание логарифмов без изменения смысла неравенства возможно, поскольку основание логарифмов больше 1.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
barina201720071 barina201720071  07.04.2021 12:40
12:х , я не понимаю как это розв язать ​...
svistmi20061 svistmi20061  07.04.2021 12:40
Реши урвнеениие 5x-4x+7=10 9+6y-5-5y=5 8x-3=5+6...
dis8 dis8  07.04.2021 12:40
Знайти координати вершин трикутника ABC1,який є образом трикутника АВС при його повороті на 90° за годинниковою стрілкою. (A(-2;2), B(0;1), C(-2;0))...
ematrenichev ematrenichev  07.04.2021 12:40
Ребята , как можно быстрее, накину максимальное кол-во , как можно быстрее ​...
ОСЕНЬ2019 ОСЕНЬ2019  07.04.2021 12:39
Катер подолав певну відстань за течією річки за 2 год., а на зворотній шлях витратив 6 год. Знайдіть швидкість течії річки, якщо власна швидкість катера дорівнює 1,8...
YankaManky YankaManky  07.04.2021 12:39
Дві кулі мають спільний центр. Знайдіть радіус більшої кулі, якщо радіус меншої кулі дорівнює 3 см, а об єм тіла, що міститься між поверхнями цих куль, дорівнює 252π...
alexbarbos75 alexbarbos75  07.04.2021 12:39
На координатной прямой отмечены точки а в и с отметьте на этой прямой число x так чтобы при этом выполнялись условия а-x 0 x-b 0 c-x 0​...
пстрвчлвяряу пстрвчлвяряу  07.04.2021 12:39
іть по брацк варіант іть ( за раня говорю пасіба ) ​...
аааликкк43527 аааликкк43527  07.04.2021 12:39
Цена на телефон снизилась на 13% какова сэкономит Мария при покупке двух телефонов по сниженней цене если первоначальная цена была 120 000 тенге?​...
nastia295 nastia295  07.04.2021 12:38
Mektep - BilimLa x +о0 https://onlinemektep.net/schedule/07.04.2021/lesson/4cd25820-90sb-45ad-a7as-37a21706c919Открыть чат5Нахождение процента от числа и числа по его...

Популярные вопросы