1.какие из пар чисел (7; 1), (8; -7; -; 3) являются решением уравнения 3х-7у=14? 2. решите систему уравнений {х-5у=23 {7х+10у=-19 3.сумма цифр двузначного числа равна 15. если поменять его цифры местами, то получим число которое меньше данного на 9.найдите данное число

№1.

Подставляем данные координаты в уравнение:

(7;1)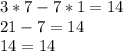

(8;2)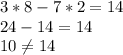

(-7;-5)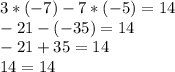

(10;3)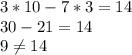

ответ: решениями уравнений являются пары (7;1) и (-7;-5)

№2.

В данном случае систему будем решать методом подстановки. Для этого выразим х из первого уравнения:

Подставляем выраженный х во второе уравнение:

Мы получили уравнение с одной переменной. Решим его, применяя стандартные правила решения уравнений с одной переменной:

Подставляем значение у в первое уравнение:

ответ: (3;-4)

№3.

Так как число дано двузначное, то 15 состоит из двух слагаемых-цифр.

Отсюда: x<10; y<10. (x и y - цифры единиц и десятков искомого числа).

При таком условии 15 можно разбить четырьмя

1) 15=9+6 (число - 96)

2) 15=6+9 (число 69)

3) 15= 8+7 (число 87)

4) 15=7+8 (число 78).

Теперь необходимо выбрать одну из двух пар чисел: 9 и 6, или 8 и 7 ?

Для этого нужно вспомнить, что искомое число на 9 больше числа, в котором поменяли цифры местами, и проверить уравнением каждую пару.

96-69=9

27≠9, следовательно данная пара цифр нам не подходит.

87-78=9

9=9 - эта пара подходит.

Так как нас спрашивали о большем числе, то ответом будет число 87.

ответ: 87.