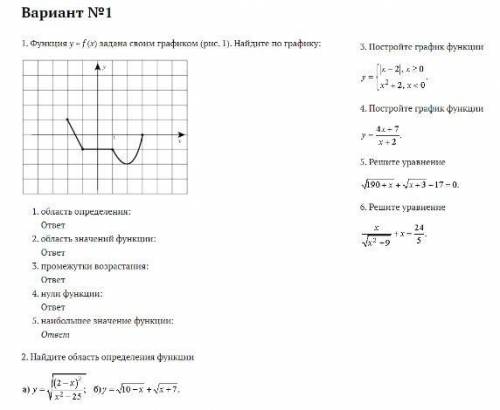
1.Функция y= f(x) задана своим графиком найдите по графику: 1) область определения, 2) область значения функции, 3) промежутки возрастания, 4) нули функции, 5) наибольшее значение функции 2. Найдите область определения функции ( примеры на фото)
3. Постройте график функции ( на фото)
4. Постройте график функции ( на фото)
5. Решите уравнение ( на фото)
6. Решите уравнение ( на фото)
Другие вопросы по теме Математика
Популярные вопросы
- Знайдіть суму перших ста членів арефметичної прогресії , якщо...
1 - решите, нужно только одно уравнение...
3 - Состояло значение битвы при Гавгамелах?...
3 - Якім чином Геродот розділив скифські племена?...
3 - необходимо перечислить все ст. из главы 2 Конституции, которым...
3 - АНГЛИЙСКИЙ СДЕЛАТЬ ДАЮ КАЖДОМУ ПО НОМЕРА 1 И 2 ТАМ ЕСТЬ И БЕЗ...
3 - За скільки років світло пролетить відстань 500 тисяч пк?...
1 - Тема. ОСНОВЫ ЗДОРОВОГО ОБРАЗА ЖИЗНИ И ЕГО ОТРАЖЕНИЕ В ПРОФЕССИОНАЛЬНОЙ...
1 - 1:Что такое мобилизация тыловые работы? 2что вы узнали о причинах...
3 - До ть знайти енергію зв язку та питому енергію зв язку ядра нітрогену...
1
2. Область значения функции y = f(x) - это множество всех значений y, которые может принимать функция. На графике можно заметить, что значения y находятся между нижней и верхней границами графика функции. Область значения функции y = f(x) будет выражаться как интервал между минимальным значением y и максимальным значением y на графике.
3. Промежутки возрастания функции можно определить, изучая наклон графика. Если график функции поднимается относительно оси x, то функция возрастает. На графике можно заметить, что функция возрастает в интервалах, где наклон графика положительный. Поэтому промежутки возрастания будут определяться интервалами, где график имеет положительный наклон.
4. Нули функции y = f(x) - это значения x, при которых функция равна нулю. На графике можно заметить, что нули функции соответствуют точкам, где график пересекает ось x. Чтобы найти эти значения x, нужно найти точки пересечения графика с осью x.
5. Наибольшее значение функции можно определить, изучая высоту графика. На графике можно заметить, что наибольшее значение функции соответствует точке на графике, где график достигает наивысшей высоты. Чтобы найти это значение, нужно найти точку на графике, где график имеет наибольшую высоту, и определить соответствующее значение y.
6. Для нахождения области определения функции по фото, необходимо предоставить фотографию с графиком функции.
7. Для построения графика функции по фото, необходимо предоставить фотографию с подробным изображением графика функции.
8. Для решения уравнения, необходимо предоставить фотографию с указанным уравнением. С помощью фото уравнения можно будет провести пошаговое решение и дать точный ответ.