1.Даны уравнения сторон треугольника: 3x+4y-1=0, x-7y-17=0, 7x+y+31=0. Доказать, что этот треугольник равнобедренный (сравнить углы).
2.Составить уравнение прямой, проходящей через две точки М1 (6;-1), М2 (9;3). Записать общее и параметрические уравнения этой прямой.
3. Записать уравнение прямой, проходящей через точку М (7;-3) с заданным угловым коэффициентом к=1/2. Привести полученное уравнение к общему виду и в отрезках на осях.

Ответы

nikitamova2004 30.12.2021 08:40

По формуле для длины отрезка находим стороны треугольника:

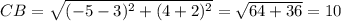
1) $CB=\sqrt{(-5-3)^{2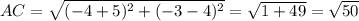}+(4+2)^{2} }=\sqrt{64+36} =10$

2) $AC=\sqrt{(-4+5)^{2}+(-3-4)^{2}}=\sqrt{1+49}=\sqrt{50}$ +

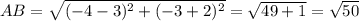3) $AB=\sqrt{(-4-3)^{2}+(-3+2)^{2} } =\sqrt{49+1}=\sqrt{50}$ +

По т.косинусов:

$AB^{2}=AC^{2}+BC^{2}-2AC*BC*cosACB\\50=50+50-2*50*cosACB\\cosACB=0,5$

cos60°=1/2, ∠CBA=∠ACB

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

апркаерн 27.11.2020 13:38

Решить графически уравнение(7)...

kola3344 27.11.2020 13:38

Чарос0302 27.11.2020 13:38

Вычисли пример и найди его сумму...

Oliichka 27.11.2020 13:37

том55551 27.11.2020 13:37

adekvat3 27.11.2020 13:37

pait 27.11.2020 13:37

ivanpanyushkin1 27.11.2020 13:37

Сл2064 27.11.2020 13:37

Г по сделаю лучшим решением ...

Артём24532523 27.11.2020 13:37