1.Дано: cos a= -0,6,П/2<а<П.Вычислите sin a, sin2a, tg(П/4+a) 2.При всех допустимых значениях a докажите тождество (на фото)

Другие вопросы по теме Математика
Популярные вопросы
- Наведіть рівняння реакцій , які дозволяють здійснити такі перетворення...
3 - Вырази из формулы длины окружности c=2\pi r длину радиуса r....
1 - Ввагоне,движущемся горизонтально с ускорением а=2 м/с висит на шнуре...
2 - Цепь питания доказывающая что в природе нет вредных организмов...
3 - 1.вычислите объем аммиака(н. при кипячении 14%-го раствора гидроксида...
2 - Сколько различных четных пятизначных чисел можно составить из цифр...
2 - Всю голову ! на ветке сидели 3000 голубей. хотели убить 2000. потом...
2 - X^-7*x^9/x^4 / т.е дробь представьте выражение в виде степени с...
3 - После разгрузки баржи её осадка в реке уменьшилась на 60 см. определите...
3 - Какой из этих фразеологизмов означает : имеющий большой жизненый...
3
1.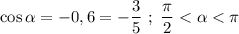 .
.
а) Так как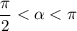 , то
, то 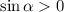 .
.
По основному тригонометрическому тождеству: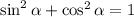 , тогда
, тогда 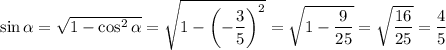 .
.
ответ: .
.
б)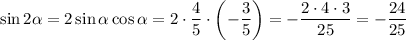 .
.
ответ: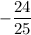 .
.
в) По формуле тангенса суммы: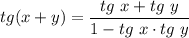 .
. 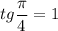 , а
, а 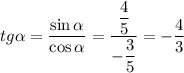 . Подставляем:
. Подставляем:
ответ: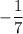 .
.
2)
Здесь мы применим формулу разности косинусов: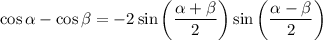 , а также формулу суммы
, а также формулу суммы
синусов: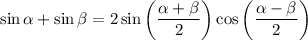 . Получаем:
. Получаем:
Так как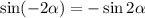 , то в числителе исчезает минус рядом с двойкой, получается:
, то в числителе исчезает минус рядом с двойкой, получается:
Сокращаем числитель и знаменатель на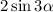 :
: