1) a+1 делиться на b, 2) a = 2b+5, 3) a+b делиться на 3, 4) a+7b=простое число. из этих утверждений три верных и одно не верное. найдите все возможные a, b

a+7b = (a+b) + 6b

если верно утверждение 3, то выражение из утверждения 4 делится на 3 и не может быть простым числом. Следовательно ложное одно из выражений 3 или 4.

Тогда и 1 и 2 верные. Подставим в первое выражение второе:

a+1 = (2b+5) +1 = 2b+6

Если оно делится на b, то на b должно делиться 6.

Следовательно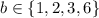

и из второго утверждения получаем пары:

Из этих пар ни для одной не выполняется утверждение 3, а следовательно будем считать именно его ложным.

четвертое утверждение неверно для первой и третьей пар и выполняется для второй и четвертой.

ответ: (9,2) и (17,6)