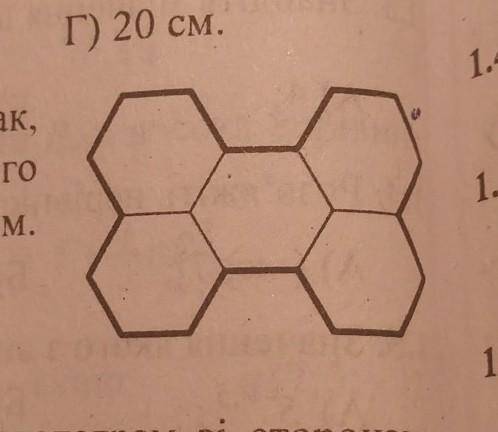
1.14. П'ять правильних шестикутників розміщено так, як показано на рисунку. Довжина кола, описаного
навколо одного з шестикутників, дорівнює 12 см.
Чому дорівнює довжина виділеної лінії?​

108/π см

Пошаговое объяснение:

1) Сторона правильного шестиугольника равна радиусу окружности, описанной около этого шестиугольника, так как:

- окружность 360° делится на 6 равных центральных углов (каждый из которых равен 360 : 6 = 60°);

- 6 образовавшихся треугольников являются равносторонними, т.к. две стороны каждого треугольника являются радиусами описанной окружности, в силу чего углы при основании равны (180 - 60) / 2 = 60°.

2) Длина выделенной линии L равна 18 радиусам описанной окружности R:

L = 18R

3) Длина окружности С и её радиус R связаны соотношением:

С = 2πR, откуда R при С = 12 см равен:

R = 12 : 2π = 6/π  см

4) Находим длину выделенной линии L:

L = 18R = 18 · (6/π) = 108/π  см  ≈ 34,4 см

ответ: длина выделенной линии равна 108/π см, или ≈ 34,4 см.