1)0,5×(-9)⁴+1,1×(-9)³-28= сколько это будет? 2)найдите значение выражения 2√6×√2×8√3= 3)окружность с центром в точке о описана около равнобедренного треугольника авс,в котором ав=вс и угол авс=124 градуса.найдите величину угла вос.ответ дайте в градусах. 4)в трапеции авсd ad=6,вс=3,а её площадь равна 27.найдите площадь треугольника авс. 5)в остроугольном треугольнике авс высота ан равна 9√39,а сторона ав равна 60.найдите cos в. 6)четырёхугольник abcd вписан в окружность.угол авс =112 градусов,угол cad=70 градусов.найдите угол abd.ответ дайте в градусах. 7)в треугольнике авс de-средняя линия.площадь треугольника cde=20.найдите площадь треугольника авс. , !

1) 0,5 · (-9)⁴ + 1,1 · (-9)³ - 28 = 0,5 · 9⁴ - 1,1 · 9³ - 28 =

 = 9³ · (0,5 · 9 - 1,1) - 28 = 9³ · (4,5 - 1,1) - 28 =

 = 9³ · 3,4 - 28 = 729 · 3,4 - 28 = 2478,6 - 28 = 2450,6

2)

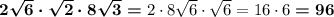
3) рис. 1

 ΔABC - равнобедренный, AB = BC,  ∠ABC = 124°  

 ⇒  ∠A = ∠BCA = (180° - ∠ABC) : 2 = (180° - 124°) : 2 = 28°

 ∠A - вписанный в окружность. равен половине центрального угла ∠BOC, который опирается на ту же дугу, что и ∠A

∠BOC = 2∠A = 2 · 28° = 56°

4) рис. 2

 Трапеция ABCD, AD║BC,  AD = 6,  BC = 3,  S = 27

 У ΔABC  и трапеции ABCD  одинаковая высота  h, которую можно найти из формулы площади трапеции :

5) рис. 3

ΔABH : ∠AHB=90°,  AB=60, AH = 9√39. Теорема Пифагора

BH² = AB² - AH² = 60² - (9√39)² = 3600 - 3159 = 441

BH = √441 = 21

6) рис.4

∠ABC - вписанный, равен половине дуги, на которую опирается.

⇒ ∪ ADC = 2∠ABC = 2 · 112° = 224°

∠CAD - вписанный, равен половине дуги, на которую опирается.

⇒ ∪ DC = 2∠CAD = 2 · 70° = 140°

∪ AD = ∪ ADC - ∪ DC = 224° - 140° = 84°

∠ABD - вписанный, равен половине дуги, на которую опирается.

⇒ ∠ABD = ∪ DC : 2 = 84° : 2 = 42°

7) рис.5

Средняя линия треугольника отсекает от него подобный треугольник, площадь которого в 4 раза меньше площади большого треугольника