0.

доказать или опровергнуть иррациональность α.

, только строгое доказательство, не "видно, же".

Допустим, что число - бесконечная периодическая дробь. Тогда, начиная с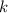 -ой цифры, некоторая последовательность из 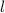цифр будет повторяться бесконечно. Очевидно, что, после 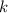-ой цифры найдутся ненулевые цифры. А значит искомый период длины 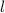содержит хотя бы одну ненулевую цифру.

Также очевидно, что в десятичной записи присутствует число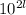 . В нем одна 1, а за ней следуют 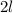нулей.

Пусть в период входят одна 1 и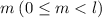 нулей этого числа. Но следующие 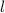цифр - нули (т.к. в предыдущее повторение периода вошло меньше, чем 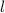нулей, незадействованными остались 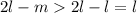подряд идущих нулей) - противоречие с тем, что в периоде есть ненулевая цифра.

А значит у дроби нет периода.

Т.к. она бесконечная (число натуральных чисел бесконечно), то иррациональная.

ответ: число иррационально