Вжесткий резервуар вместимостью 3 м3 компрессором нагнетается азот (n2), избыточное давление в резервуаре повышается от 0,2 до 2,5 бар, а температура от 25 до 75 ос. барометрическое давление bо=750 мм рт.ст. определить массу азота, поступившего в резервуар. считать азот идеальным газом. ответ: m=6,1 кг
Другие вопросы по теме Химия
Популярные вопросы
- Етилметаноат належить до класу: А. Жирів. Б. Естерів. В. Алканів. Г. Спиртів....
3 - Назвіть рослинне угруповання в якому панують багаторічні трав’янисті рослини,...
1 - Нужна с тестом по русскому языку. ответ может быть не 1...
3 - Окислительно-восстановительной является реакция: 1.2NaHCO3 → Na2CO3 + CO2 + H2O...
3 - Подскажите какая версия Майнкрафта лучше всего для одиночного прохождения с модами?...
1 - Установіть відповідність між типами режиму річок України та їх живленням.1 Східноєвропейський2...
1 - 1. Определить количество вещества 4 г. NaOH. 2. Какую массу будут иметь 10 моль...
1 - Для виготовлення фарфору беруть 25 частин білої глини, 2 частини піску й 1 частину...
3 - Усі хвойні дерева є вічнозеленими? будь ласка до ть дуже терміново ів тільки...
1 - Встановіть відповідність між біосферними заповідниками України та їх характерними...
1
Дано:
V = 3 м³
Ратм = 750 мм. рт. ст. = 99991 Па ≈ 10⁵ Па
Р₁ = 0,2 бар = 0,2*10⁵ Па
Р₂ = 2,5 бар = 2,5*10⁵ Па
Т₁ = 25°С = 298°К
Т₂ = 75°С = 348°К
Найти: Δm(N₂) - ?
1) Манометр в резервуаре показывает избыточное давление. Находим абсолютное давление азота в резервуаре до и после закачивания газа:
Р₁ = 0,2*10⁵ + 10⁵ = 1,2*10⁵ Па
Р₂ = 2,5*10⁵ + 10⁵ = 3,5*10⁵ Па
2) Уравнение 2) Уравнение Менделеева-Клапейрона для идеального газа:
Р*V = (m/M)*R*T
где: Р - давление газа , Па.
V - объем газа, м³
m - масса газа, кг
М - масса 1 моля газа, кг/моль.
М(N₂) = 2*14 = 28 г/моль = 0,028 кг/моль
R - универсальная газовая постоянная, R = 8,314 Дж/(моль*К)
T - температура, °К.
3) Из уравнения Менделеева-Клапейрона определяем массу газа
до и после закачивания:
Отсюда: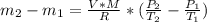
\\
ответ: 6,093 кг