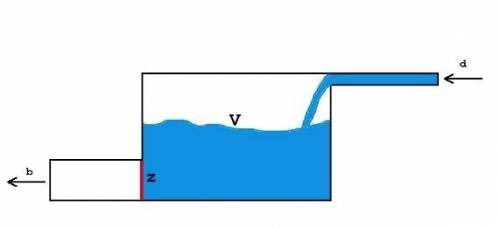
Задача D. Водопровод с резервной ёмкостью Рассмотрим следующую модель водопровода. Имеется резервная ёмкость объемом V литров. По входной трубе постоянно поступает вода со скоростью d литров в минуту. По выходной трубе жидкость выливается со скоростью b литров в минуту. Выполняется условие, что d < b. В начальный момент времени выход Z из ёмкости перекрыт. В тот момент, когда ёмкость наполняется, выход открывается и вода поступает на выпуск. Так как d < b, то в какой-то момент ёмкость полностью опустеет, и заслонка Z снова закрывается, после чего процесс повторяется снова.

Очевидно, что при этом в работе водопровода случаются паузы, в течение которых происходит заполнение резервной ёмкости. К ним относится и первая пауза, служащая для первичного наполнения ёмкости водой. По техническим причинам требуется, чтобы длина каждой такой паузы не превышала величины p. При этом нас интересует суммарное время t, в течение которого выходная труба была открыта. Количество пауз n при этом должно быть минимальным возможным.

В рассматриваемой модели используются сколь угодно малые доли времени и объема. Считается, что заслонка Z срабатывает мгновенно.

По заданным величинам d, b, t, p требуется найти такой целый объём V, при котором число пауз n было минимально возможным для заданного времени подачи воды t, а среди всех объёмов, обеспечивающих такое время работы подачи воды и такое количество пауз найти самый маленький.

Формат входных данных

В первой строке содержится четыре целых числа d, b, t, p через пробел :

1

≤

1≤ d < b

≤

2

∗

1

0

9

≤2∗10

9

,

1

≤

1≤ t

≤

15000

≤15000,

1

≤

1≤ p

≤

5000

≤5000.

Формат выходных данных

Вывести одно целое число - объем V резервной ёмкости, обеспечивающей необходимые ограничения на подачу воды. Если таких объёмов несколько, вывести минимальный.

Пояснение к примеру 1.

Рассмотрим первый пример из условия. Скорость подачи d равна 5 литров в минуту, скорость выпуска b равна 10 литров в минуту, требуется обеспечить суммарную работу выпуска в течение t = 32 минут, при этом максимальный размер любой паузы не должен превышать p = 8 минут.

Если мы установим объём резервной ёмкости 40 литров, то:

- ровно за 8 минут (что разрешено условием) она наполнится со скоростью 5 литров в минуту;

- далее пойдет процесс выпуска: 40 литров будут выпущены за 4 минуты со скоростью выпуска 10 литров в минуту, но за это время в ёмкость попадёт 4*5 = 20 литров новой воды. Она будет выпущена за 2 минуты, но за это время поступит 2*5 = 10 литров новой воды, которая будет выпущена за 1 минуту и так далее. Так как доли времени и объема могут быть сколь угодно малыми, получим при подсчёте времени работы выпуска следующую сумму: 4 + 2 + 1 + 0.5 + 0.25 + 0.125 + , которая в итоге равна 8. То есть через 8 минут ёмкость полностью опустеет и заслонка закроется. Для того, чтобы время работы выпуска было равно 32 минуты потребуется 32 / 8 = 4 таких цикла, а значит и 4 паузы. За меньшее число пауз работу выпуска в течение 32 минут при существующих ограничениях обеспечить не получится.

Очевидно, что V = 40 литров - максимально возможный разрешённый объём, иначе первая же пауза будет больше допустимой. С другой стороны, если мы попробуем уменьшить объем до 39 литров, то получим:

- первоначальное заполнение будет произведено за 39 / 5 = 7.8 минуты. Далее процесс выпуска будет работать 39/10 + 39/20 + 39/40 + ... = 7.8 минуты. Тогда за 4 цикла выпуск будет работать 31.2 минуты и для обеспечения 32 минут работы выпуска потребуется пятая пауза.

Sample Input 1:

5 10 32 8

Sample Output 1:

40

Sample Input 2:

5 10 30 8

Sample Output 2:

38

Sample Input 3:

127 128 1 1

Sample Output 3:

1
На Python 3

тетрадка535243    1   16.10.2020 06:53    6