, Задача 9. Счастливая подстрока ( ) Поликарп выписал на доске n цифр, отличных от нуля. Таким образом, на доске записана строка s длины n, состоящая из цифр от 1 до 9.
Введем понятие подстроки строки s: подстрока строки s — это последовательность, состоящая из произвольного количества символов строки s, которые идут в строке s подряд.
Теперь он хочет найти в этой строке подстроку максимальной длины, которая удовлетворяет следующим условиям:
• длина подстроки — четное число;
• пусть x — длина подстроки, тогда сумма первых x/2 цифр подстроки равна сумме
последних x/2 цифр подстроки.
Перед вами стоит задача определить максимальную длину подстроки строки s, которая
удовлетворяет описанным условиям.
Формат входных данных
В первой строке следует целое число n (2 6 n 6 5 000) — длина строки s.
Во второй строке следует строка s длины n, состоящая из цифр от 1 до 9.
Формат выходных данных
Выведите максимальную длину подстроки строки s, которая удовлетворяет описанным
условиям. Если ни одной подходящей подстроки не существует, выведите 0.

Замечание
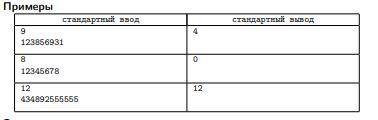
В первом примере ответной подстрокой является подстрока 3856 длины 4, которая начинается в позиции 3 и заканчивается в позиции 6. Сумма первой половины цифр равна
11 и сумма второй половины цифр равна 11, поэтому эта подстрока удовлетворяет всем
условиям.
Во втором примере нет ни одной подстроки, удовлетворяющей всем условиям, поэтому
нужно вывести 0.

Vikamolch11    3   13.12.2021 12:26    3