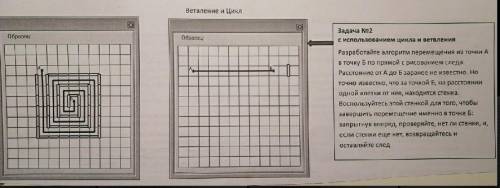
Задача №2 с использованием цикла и ветвления Разработайте алгоритм перемещения из точки А в точку Б по прямой с рисованием следа. Расстояние от Адо Б заранее не известно. Но точно известно, что за точкой Б, на расстоянии одной клетки от нее, находится стенка. Воспользуйтесь этой стенкой для того, чтобы завершить перемещение именно в точке Б: запрыгнув вперед, проверяйте, нетли стенки, и, если стенки еще нет, возвращайтесь и оставляйте след​

Хорошо, давайте разработаем алгоритм перемещения из точки А в точку Б с использованием цикла и ветвления:

1. Определите начальные координаты точки А и точки Б. Например, можно представить точки А и Б как две переменные с их координатами (xA, yA) и (xB, yB) соответственно.

2. Создайте переменную, которая будет отвечать за перемещение вперед. Для этого можно установить значение equalForward равным 1.

3. Создайте цикл, который будет выполняться до тех пор, пока xA не будет равно xB. Внутри цикла будут выполняться следующие действия:

a) Проверьте, находится ли в точке (xA+equalForward, yA) стенка. Для этого можно использовать условный оператор if. Если есть стенка, выполните шаг d), если нет стенки, выполните шаг b).

b) Увеличьте значение xA на equalForward (xA = xA + equalForward). Это перемещает точку А вперед на одну клетку.

c) Нарисуйте след точки А на доске, например, можно показать его символом "*".

d) Уменьшите значение equalForward на 1 (equalForward = equalForward - 1). Это позволит в следующей итерации цикла выполнить перемещение назад на одну клетку.

e) Нарисуйте след точки А на доске, как и в шаге c).

4. После завершения цикла, точка А будет находиться в точке Б, и вы можете написать, что перемещение завершено.

Объяснение и обоснование решения:

- В начале алгоритма мы устанавливаем значение equalForward равным 1, чтобы сначала переместиться вперед на одну клетку.
- Затем мы создаем цикл, который выполняется до тех пор, пока точка А не достигнет точки Б. Это обеспечивает постепенное перемещение точки А по прямой с рисованием следа.
- Внутри цикла мы проверяем наличие стенки в следующей точке и соответствующим образом перемещаемся вперед или назад, чтобы оставить след. Это гарантирует, что перемещение завершится именно в точке Б.
- Рисование следа осуществляется путем пометки каждой посещенной клетки символом "*". Это позволяет визуально представить путь перемещения.

Шаг за шагом решение:

Предположим, начальные координаты точек А и Б такие:
- Точка А: xA = 2, yA = 1
- Точка Б: xB = 7, yB = 1

1. Установим equalForward равным 1.

2. Создадим цикл, который будет выполняться до тех пор, пока значение xA не будет равно xB. Сейчас xA не равно xB, поэтому переходим к выполнению следующих шагов.

a) Проверим наличие стенки в точке (3, 1). Нет стенки.
b) Увеличим xA на equalForward. Теперь xA = 3, yA = 1.
c) Нарисуем след точки А на доске.
d) Уменьшим equalForward на 1. Теперь equalForward = 0.
e) Нарисуем след точки А на доске.

3. Возвращаемся к началу цикла.

a) Проверим наличие стенки в точке (4, 1). Есть стенка.
b) Увеличиваем xA на equalForward (что равно 0). Теперь xA остается равным 3, yA остается равным 1.
c) Не рисуем след точки А на доске.
d) Уменьшаем equalForward на 1. Теперь equalForward становится равным -1.
e) Не рисуем след точки А на доске.

4. Возвращаемся к началу цикла.

a) Проверяем наличие стенки в точке (2, 1). Нет стенки.
b) Увеличиваем xA на equalForward. Теперь xA становится равным 2, yA остается равным 1.
c) Рисуем след точки А на доске.
d) Уменьшаем equalForward на 1. Теперь equalForward становится равным -2.
e) Рисуем след точки А на доске.

5. Возвращаемся к началу цикла.

a) Проверяем наличие стенки в точке (1, 1). Нет стенки.
b) Увеличиваем xA на equalForward. Теперь xA становится равным 0, yA остается равным 1.
c) Рисуем след точки А на доске.
d) Уменьшаем equalForward на 1. Теперь equalForward становится равным -3.
e) Рисуем след точки А на доске.

6. Возвращаемся к началу цикла.

a) Проверяем наличие стенки в точке (-1, 1). Нет стенки.
b) Увеличиваем xA на equalForward. Теперь xA становится равным -1, yA остается равным 1.
c) Рисуем след точки А на доске.
d) Уменьшаем equalForward на 1. Теперь equalForward становится равным -4.
e) Рисуем след точки А на доске.

7. Возвращаемся к началу цикла.

a) Проверяем наличие стенки в точке (-2, 1). Нет стенки.
b) Увеличиваем xA на equalForward. Теперь xA становится равным -2, yA остается равным 1.
c) Рисуем след точки А на доске.
d) Уменьшаем equalForward на 1. Теперь equalForward становится равным -5.
e) Рисуем след точки А на доске.

8. Возвращаемся к началу цикла.

a) Проверяем наличие стенки в точке (-3, 1). Нет стенки.
b) Увеличиваем xA на equalForward. Теперь xA становится равным -3, yA остается равным 1.
c) Рисуем след точки А на доске.
d) Уменьшаем equalForward на 1. Теперь equalForward становится равным -6.
e) Рисуем след точки А на доске.

9. Возвращаемся к началу цикла.

a) Проверяем наличие стенки в точке (-4, 1). Нет стенки.
b) Увеличиваем xA на equalForward. Теперь xA становится равным -4, yA остается равным 1.
c) Рисуем след точки А на доске.
d) Уменьшаем equalForward на 1. Теперь equalForward становится равным -7.
e) Рисуем след точки А на доске.

10. Возвращаемся к началу цикла.

a) Проверяем наличие стенки в точке (-5, 1). Есть стенка!
b) Увеличения xA на equalForward (что равно -7). Теперь xA остается равным -4, yA остается равным 1.
c) Не рисуем след точки А на доске.
d) Уменьшаем equalForward на 1. Теперь equalForward становится равным -8.
e) Не рисуем след точки А на доске.

11. Выходим из цикла, так как xA равно xB (т.е. -4 равно 7). Перемещение завершено.

Таким образом, алгоритм будет перемещать точку А по прямой с рисованием следа, используя стенку чтобы добраться до точки Б. В конечном итоге точка А будет находиться в точке Б.