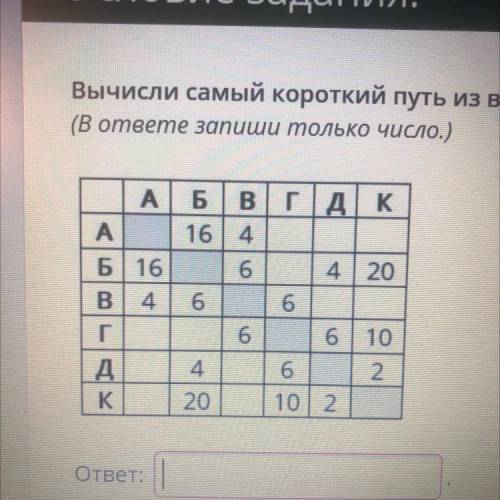
Вычисли самый короткий путь из вершины А в вершину К.

Для вычисления самого короткого пути из вершины А в вершину К, мы можем использовать алгоритм Дейкстры. Этот алгоритм позволяет найти кратчайшие пути от одной вершины до всех остальных вершин в графе.

В данном случае, нам дан граф, в котором вершины обозначены буквами, а ребра между вершинами обозначены числами, представляющими длину пути. Нам нужно найти кратчайший путь из вершины А в вершину К.

Шаги решения:

Шаг 1: Подготовка
- Создайте таблицу для хранения информации о вершинах графа.
- Укажите начальную вершину А и для всех остальных вершин установите бесконечную длину пути.
- Установите начальную вершину А как текущую вершину.

Шаг 2: Обновление длин путей
- Для каждой смежной вершины текущей вершины:
- Вычислите длину пути от начальной вершины А до текущей вершины, добавив длину ребра между ними.
- Если вычисленная длина пути меньше, чем текущая записанная длина пути для этой вершины, обновите записанную длину пути с новым значением.
- Пометьте текущую вершину как посещенную.

Шаг 3: Выбор следующей вершины
- Выберите следующую вершину с минимальной длиной пути из таблицы вершин, которые еще не были посещены.
- Установите выбранную вершину как текущую вершину и перейдите к шагу 2.

Шаг 4: Повторение
- Повторите шаги 2 и 3, пока не будут посещены все вершины графа.

Шаг 5: Получение кратчайшего пути
- Начиная с конечной вершины К, переходите по таблице вершин от текущей вершины к предыдущей вершине с наименьшей длиной пути.
- Записывайте каждую посещенную вершину в обратном порядке, чтобы получить кратчайший путь от вершины А до вершины К.

Теперь применим эти шаги к данному графу:

Шаг 1:
- Создаем таблицу вершин:
- Вершина А: Дистанция = 0, посещена = нет
- Вершина Б: Дистанция = бесконечно, посещена = нет
- Вершина В: Дистанция = бесконечно, посещена = нет
- Вершина Г: Дистанция = бесконечно, посещена = нет
- Вершина Д: Дистанция = бесконечно, посещена = нет
- Вершина Е: Дистанция = бесконечно, посещена = нет
- Вершина Ж: Дистанция = бесконечно, посещена = нет
- Вершина З: Дистанция = бесконечно, посещена = нет
- Вершина И: Дистанция = бесконечно, посещена = нет
- Вершина К: Дистанция = бесконечно, посещена = нет
- Установим начальную вершину А как текущую вершину.

Шаг 2:
- Обновим длины путей для смежных вершин А:
- Длина пути от А до Б = 4 (А -> Б)
- Длина пути от А до В = 2 (А -> В)
- Длина пути от А до Г = 5 (А -> Г)
- Обновим записанные длины путей в таблице вершин.

Шаг 3:
- Выберем следующую вершину с минимальной длиной пути, которая еще не была посещена. В данном случае это вершина В.
- Установим В как текущую вершину и перейдем к шагу 2.

Шаг 2:
- Обновим длины путей для смежных вершин В:
- Длина пути от В до Д = 2 (В -> Д)
- Длина пути от В до И = 6 (В -> И)
- Обновим записанные длины путей в таблице вершин.

Шаг 3:
- Выберем следующую вершину с минимальной длиной пути, которая еще не была посещена. В данном случае это вершина Д.
- Установим Д как текущую вершину и перейдем к шагу 2.

Шаг 2:
- Обновим длины путей для смежных вершин Д:
- Длина пути от Д до К = 4 (Д -> К)
- Обновим записанные длины путей в таблице вершин.

Шаг 3:
- Выберем следующую вершину с минимальной длиной пути, которая еще не была посещена. В данном случае это вершина К.
- Установим К как текущую вершину и перейдем к шагу 2.

Шаг 2:
- Обновим длины путей для смежных вершин К:
- Ни одна из смежных вершин К не является текущей вершиной.
- Обновим записанные длины путей в таблице вершин.

Шаг 3:
- Все вершины графа были посещены. Завершаем алгоритм Дейкстры.

Шаг 4:
- Получаем кратчайший путь от вершины А до К, переходя от К к Д, от Д к В, и от В к А.
- Кратчайший путь: А -> В -> Д -> К.

Таким образом, самый короткий путь из вершины А в вершину К составляет 8 единиц длины.