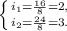Вес одного символа 6 битов, символов в сообщении 40. Определите мощность алфавита и информационный объем текста(в байтах)
2. Дано сообщений объемом 0,5 Кбайт. Количество страниц 2, строк 16, символов в строке 32. Найти мощность алфавита
3. Дано два закодированных сообщений: АБВ13КЛ47БА и 25КЛМ39РПА. Они весят 176 бит и 240 бит соответственно. Найти вес одного символа в каждом сообщении. ответ выразите в байтах
​

1. Мощность - 64 символа, Объем информации - 30 байт

2. 16 символов

3. 2 и 3 байта соответственно

Объяснение:

1. Формула(Ф1) объема информации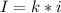 , где I - объем в битах, k - количество символов, i - вес одного символа. Подставляем значения: I=40*6=240бит. Т.к. 1байт = 8 бит, то I= 240/8=30 байт.

Мощность алфавита (N) вычисляется по формуле(Ф2)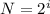 , где i - информационный вес одного символа. Подставляем значения: 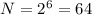символа.

2. Объем сообщения 0,5 КБайта, а т.к 1 КБ=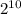 байт = 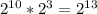бит, то объем сообщения равен 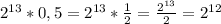бит.

Количество символов в тексте = кол-во символов в строке * кол-во строк * кол-во страниц =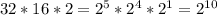 символов.

По формуле Ф1 получаем, что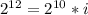 , откуда вес одного символа равен 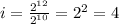бита.

По формуле Ф2 получаем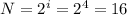 символов

3. Объем первого сообщения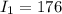 бит, второго - 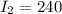бит. Количество символов первого сообщения 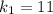символов, второго - 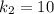символов. По формуле Ф1 получаем, что 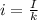. Подставляем значения: 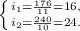полученные значения в БИТАХ.

т.к. 1 байт = 8 бит, то получаем значения в байтах