Упростите логические выражения(нужен не только ответ, но и решение)
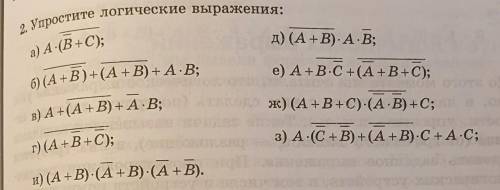
Другие вопросы по теме Информатика
Популярные вопросы
- У трикутнику MNL кут M = куту N = 50°. NК – бісектриса, MК =...
3 - 1. Some tribes were more interested in for the English * fighting...
1 - Complete the travel blog. Use the comparative form of the adjectives...
2 - Чи є пара чисел (-2; 1) розв язком системи рівнянь x²-y²=33x+y=7якщо...
2 - 5. « Әлеуметтік желілер - уақыт ұрлаушылар ма?» деген сұраққа...
1 - С высотой атмосфера становится и постепенно переходит в межпланетное...
1 - Напишите интервью с сотрудником Мит о изменении курса...
1 - Найдите найти площадь отличным...
1 - Составь из слов предложение! Найди лишнее слово и отметь его!...
2 - Нужно из текста выписать предложения с ПО и разобрать ,...
1
Первое, что нам нужно сделать, это привести выражение к основным операциям логики: конъюнкция (логическое "И"), дизъюнкция (логическое "ИЛИ"), и отрицание (логическое "НЕ").
1. Давайте начнем со скобок. Мы видим две пары скобок в выражении, поэтому в первую очередь решим выражения в этих скобках.
- Сначала рассмотрим первые две скобки:
(А ∨ В) ∧ (Р ∨ Ц)
В этих скобках у нас есть дизъюнкция (логическое "ИЛИ"), поэтому мы должны провести эту операцию для значений А и В, а также Р и Ц. Предположим, что A = 1, B = 0, R = 1 и C = 1 (здесь 1 обозначает верное утверждение, а 0 - неверное).
(1 ∨ 0) ∧ (1 ∨ 1)
Выполним операции для каждой пары значений:
1 ∨ 0 = 1 (так как хотя бы одно из утверждений верно)
1 ∨ 1 = 1 (так как хотя бы одно из утверждений верно)
Таким образом, получаем:
(1) ∧ (1) = 1 (так как оба утверждения истинные)
- Теперь рассмотрим следующую пару скобок:
(X ∨ Y) ∨ Z
У нас снова есть дизъюнкция (логическое "ИЛИ"), поэтому мы проводим операцию для значений X и Y, а затем для результата с Z. Предположим, что X = 0, Y = 1 и Z = 0.
(0 ∨ 1) ∨ 0
Выполняем операцию для каждой пары значений:
0 ∨ 1 = 1 (так как хотя бы одно из утверждений верно)
1 ∨ 0 = 1 (так как хотя бы одно из утверждений верно)
Таким образом, получаем:
(1) ∨ 0 = 1 (так как хотя бы одно из утверждений верно)
2. Теперь, когда у нас осталось два значения - одно в скобках и одно снаружи - мы можем решить логическую операцию для этих двух значений. У нас здесь есть конъюнкция (логическое "И").
Рассмотрим два значения:
(1) ∧ 1 = 1 (так как оба утверждения верны)
3. В результате, мы получаем ответ:
1 ∧ 1 = 1 (так как оба утверждения истинные)
Таким образом, упрощенное логическое выражение равно 1.