Упростить логическое выражение: 1) A+B+!A
2)(A#B)+(A#!B)
3)(A+B)#(A+C)
! - отрицание (не)
+ - дизъюнкция (или)
# - исключающее или, сумма по модулю 2 (XOR)
(Заранее большое)
Другие вопросы по теме Информатика
Популярные вопросы
- решить задание, расписав формулы для расчёта задания в exсel...
2 - Прочитайте текст. Определите тип речи и стиль. Выделите основную инфор- мацию...
2 - основою піраміди є прямокутник abcd сторона ab=7 см діагональ bd=25см. знайти...
3 - Чому гнів є дуже шкідливою та руйнівного емоцією?...
2 - Обдуваемый ветром он все-таки шёл вперёд не обращая внимание на непогоду....
1 - На предприятии работает 10 рабочих. И каждый рабочий получает а зарплату....
2 - Яка кількість теплоти виділяється у разі згорання 2 кг торфу...
1 - Phyton:Даны натуральное число N и вещественное число X. Вычисли: 1+x+x^2/2!+x^3/3!+...+x^n/n!...
3 - З якою силою відштовхуються два електрони , які знаходяться один від одного...
1 - Составить 2 частушки из 4 строк. одна рандом про школу Вторая должна начинаться...
1
(закон исключенного третьего: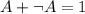 ; операция с константой:
; операция с константой: 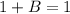 )
)
(заменяю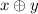 на
на 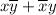 ; дальше, пользуясь сочетательным и распределительным законами и законом двойного отрицания, применяю закон исключенного третьего)
; дальше, пользуясь сочетательным и распределительным законами и законом двойного отрицания, применяю закон исключенного третьего)
(всё вышеперечисленное, только добавляю законы де Моргана для раскрытия скобок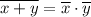 )
)