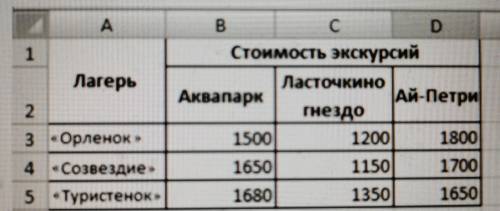
Три детских лагеря — «Орленок», «Созвездие», «Туристенок» (Крым) — ежедневно принимают соответственно 30, 20 и 16 человек. Экскурсионная программа каждой группы
состоит из посещения аквапарка, посещения Ласточкиного
гнезда и путешествия на гору Ай-Петри. Стоимость экскурсий на человека для разных лагерей приведена на рис. П6.17.
При этом существуют ограничения на количество человек в экскурсии: аквапарк — 25, Ласточкино гнездо — 20,
Ай-Петри — 30 человек. От каждого лагеря на каждую экскурсию должно быть послано не менее 5 человек. Определите
оптимальное количество учеников для участия в каждой
экскурсии при заданных ограничениях, чтобы суммарные
расходы родителей были минимальны.
Другие вопросы по теме Информатика
Популярные вопросы
- Дано вибірку:4;5;4;4;3;2;4;3;5;3. Знайдіть відносну частоту.а)...
3 - До ть будь ласка, буду вдячний! С малюнком будь ласка...
3 - СОР ПО ВСЕМИРНОЙ ИСТОРИИ! Определите значение термина демократия...
2 - Найдите значение выражения (9.9*10^2):(1.2*10^-1)=...
1 - Для домашнего задания по познанию мира Марат собрал 1,5 кг лекарственных...
2 - 80% болшек туринде жазыныз...
2 - Закончите уравнения реакций: 1) Mg+ H2SO4→ 2) NaOH+ H3PO4 → 3)...
3 - Метод навчання оповідання здобування знань по краплині плейтена...
2 - Напишіть рівняння реакцій взаємодії воді із запропонованими речовинами:...
2 - РУССКИЙ ЯЗЫК У меня экзамен))...
3
1. Составим математическую модель задачи.
Пусть:
x1 - количество учеников из лагеря "Орленок" для посещения аквапарка
x2 - количество учеников из лагеря "Орленок" для посещения Ласточкиного гнезда
x3 - количество учеников из лагеря "Орленок" для путешествия на гору Ай-Петри
x4 - количество учеников из лагеря "Созвездие" для посещения аквапарка
x5 - количество учеников из лагеря "Созвездие" для посещения Ласточкиного гнезда
x6 - количество учеников из лагеря "Созвездие" для путешествия на гору Ай-Петри
x7 - количество учеников из лагеря "Туристенок" для посещения аквапарка
x8 - количество учеников из лагеря "Туристенок" для посещения Ласточкиного гнезда
x9 - количество учеников из лагеря "Туристенок" для путешествия на гору Ай-Петри
Тогда наша целевая функция будет иметь вид:
Z = 300x1 + 400x2 + 500x3 + 250x4 + 350x5 + 450x6 + 200x7 + 300x8 + 400x9
Имеем следующие ограничения:
x1 + x2 + x3 ≥ 5 (ограничение на количество учеников из лагеря "Орленок" для всех экскурсий)
x4 + x5 + x6 ≥ 5 (ограничение на количество учеников из лагеря "Созвездие" для всех экскурсий)
x7 + x8 + x9 ≥ 5 (ограничение на количество учеников из лагеря "Туристенок" для всех экскурсий)
x1 + x4 + x7 ≤ 25 (ограничение на количество учеников для посещения аквапарка)
x2 + x5 + x8 ≤ 20 (ограничение на количество учеников для посещения Ласточкиного гнезда)
x3 + x6 + x9 ≤ 30 (ограничение на количество учеников для путешествия на гору Ай-Петри)
2. Решаем симплекс-методом.
Приводим систему ограничений к каноническому виду, добавляя вспомогательные переменные, и записываем симплекс-таблицу.
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | RHS |
|-------|------------|----------|----------|----------|---------|----------|----------|---------|----------|--------|
| s1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 5 |
| s2 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 5 |
| s3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 5 |
| s4 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 25 |
| s5 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 20 |
| s6 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 30 |
| Z | -300 | -400 | -500 | -250 | -350 | -450 | -200 | -300 | -400 | 0 |
Анализируем коэффициенты у целевой функции Z. Видим, что есть отрицательные коэффициенты, что означает, что можно улучшить текущее решение. Ищем в разрешающем столбце элемент с наименьшим отношением RHS/коэффициент у целевой функции Z. В данном случае это s4.
3. Проводим итерацию симплекс-метода.
Подставляем разрешающий элемент вместо ведущего и выражаем новую ведущую строку.
Новую симплекс-таблицу получим следующей:
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | RHS |
|-------|------------|----------|----------|----------|---------|----------|----------|---------|----------|--------|
| s1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 5 |
| s2 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 5 |
| s3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 5 |
| x4 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 25 |
| s5 | -1 | 1 | 0 | -1 | 1 | 0 | -1 | 1 | 0 | -5 |
| s6 | -1 | 0 | 1 | -1 | 0 | 1 | -1 | 0 | 1 | 5 |
| Z | -500 | -100 | -200 | -100 | -100 | -200 | -100 | -200 | -100 | 500 |
Видим, что все коэффициенты у целевой функции Z положительные или равны 0. Это означает, что оптимальное решение найдено.
4. Анализируем полученное оптимальное решение.
В соответствии с оптимальным решением, количество учеников для участия в каждой экскурсии для каждого лагеря будет следующим:
- Лагерь "Орленок":
- Аквапарк: 5 учеников
- Ласточкино гнездо: 0 учеников
- Гора Ай-Петри: 20 учеников
- Лагерь "Созвездие":
- Аквапарк: 0 учеников
- Ласточкино гнездо: 5 учеников
- Гора Ай-Петри: 0 учеников
- Лагерь "Туристенок":
- Аквапарк: 20 учеников
- Ласточкино гнездо: 15 учеников
- Гора Ай-Петри: 5 учеников
Таким образом, оптимальное количество учеников для участия в каждой экскурсии при заданных ограничениях, чтобы суммарные расходы родителей были минимальны, будет следующим:
- Аквапарк: 5 учеников из лагеря "Орленок" и 20 учеников из лагеря "Туристенок"
- Ласточкино гнездо: 5 учеников из лагеря "Созвездие" и 15 учеников из лагеря "Туристенок"
- Гора Ай-Петри: 20 учеников из лагеря "Орленок" и 5 учеников из лагеря "Туристенок"