Решите на пайтон Элементами множеств А, P, Q являются натуральные числа, причём P = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21}, Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}. Известно, что выражение
((x ∈ P) → (x ∈ A)) ∨ (¬(x ∈ A) → ¬(x ∈ Q))
истинно ( т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.
Другие вопросы по теме Информатика
Популярные вопросы
- Оқы , қажетті суретті жапсыр...
3 - Человеческое убожество-это метафора?...
3 - Визнач, до яких явищ природи відноситься процес: «шелестить...
3 - Основи прямокутної трапеції =3см, 7см більша бічна сторона 5см...
2 - Эссе Как последствия научно- технического прогресса 20 века...
3 - Сравни1000см³-1дм³ и 800м²:4м²2000дм³+200м³ и 200см³+2000см³...
2 - Сообщение добывания пищи животными не мало не много...
2 - Have you all the food A) eat b) ate C) eaten...
1 - Итальянский путешественник, иследователь Китая, Индии. Первым...
2 - 2.Знайти площу прямокутної трапеції, якщо її основи дорівнюють...
1
p = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]
q = [3, 6, 9, 12, 15, 18, 21, 24, 27, 30]
ans = 0
for x in range(30):
if (x in p) and (x in q):
ans += x
print(ans)
Объяснение:
Это логическое выражение, где переменными выступают выражения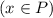 ,
, 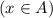 и
и 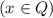 . Обозначим их за
. Обозначим их за 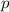 ,
,  и
и 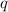 соответственно. Например,
соответственно. Например, 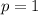 , если
, если  , и
, и 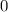 иначе. У нас получается следующее выражение:
иначе. У нас получается следующее выражение:
Раскроем импликацию и получим:
Уберём повторяющуюся . Наше финальное выражение:
. Наше финальное выражение:
Таким образом, выражение из условия будет истинно, если число не принадлежит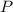 , или не принадлежит
, или не принадлежит 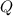 , или принадлежит
, или принадлежит 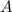 . Множество
. Множество 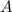 наименьшего размера будет содержать все числа, которые не удовлетворяют условию
наименьшего размера будет содержать все числа, которые не удовлетворяют условию 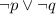 , то есть все числа, которые принадлежат и
, то есть все числа, которые принадлежат и 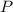 , и
, и 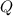 .
.