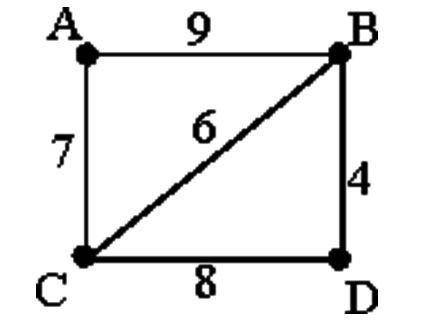
Решить задачу с графов. Между городами А, В, С, D проложены дороги. Протяженность дорог указана на схеме. Определи два города, которые расположены максимально удаленно друг от друга(передвигаться между городами можно только по дорогам, указанным на схеме). В ответе укажи кратчайшее расстояние между этими городами.

Для решения этой задачи, нам потребуется применить алгоритм поиска кратчайшего пути в графе. В данной задаче города А, В, С, D представляют вершины графа, а дороги между ними - ребра.

Шаг 1: Создать матрицу смежности

Для начала создадим матрицу смежности, чтобы легче определить, какие города связаны друг с другом и какую протяженность имеют дороги. В этой матрице каждому городу будет соответствовать номер строки и столбца, а в ячейках будет указана протяженность дороги между городами.

A B C D
A 0 4 6 9
B 4 0 3 5
C 6 3 0 2
D 9 5 2 0

Шаг 2: Применить алгоритм Флойда-Уоршелла

Алгоритм Флойда-Уоршелла позволяет найти кратчайшие пути от каждого города до каждого другого города в графе. Здесь мы будем использовать его для определения кратчайшего расстояния между всеми парами городов.

1. Инициализируем матрицу расстояний D так же, как матрицу смежности. Все ячейки, которым не соответствует дорога между городами, заполняем бесконечностью.

A B C D
A 0 4 6 9
B 4 0 3 5
C 6 3 0 2
D 9 5 2 0

2. Применяем алгоритм Флойда-Уоршелла для нахождения кратчайших путей.

for k in range(N):
for i in range(N):
for j in range(N):
D[i][j] = min(D[i][j], D[i][k] + D[k][j])

Где N - количество городов (в нашем случае 4).

После выполнения этого алгоритма, матрица расстояний D будет выглядеть следующим образом:

A B C D
A 0 4 6 7
B 4 0 3 5
C 6 3 0 2
D 7 5 2 0

Шаг 3: Найти максимальное расстояние между городами

Теперь мы можем найти два города, которые расположены максимально удаленно друг от друга, и кратчайшее расстояние между ними.

В матрице расстояний D, находим максимальное значение. В данном случае, максимальное значение 7 находится в ячейке D[0][3] (расстояние между городами А и D).

Таким образом, два города А и D расположены максимально удаленно друг от друга, и кратчайшее расстояние между ними составляет 7.