Решить ! ! мистер фокс записал выражение: 2⋅(2⋅(2⋅(…2⋅(2+1)…)+1)+1)+1, в котором 2017 двоек, вычислил его, результат перевел в двоичную систему счисления. затем он подсчитал количество единиц в получившемся двоичном числе. что у него получилось? комментарий. если бы он использовал три двойки, то выражение выглядело бы так: 2⋅(2⋅(2+1)+1)+1.
Другие вопросы по теме Информатика
Популярные вопросы
- Нужно.! выпишите из текста прилагательные с существительными,к...
3 - Подчеркните главные члены предложения.за веной,красой природы,лето...
1 - Округлите следующие числа: до едениц: 85,3 0,8 6,5 5,4 0,797...
2 - Напесать предложение 5-6 о зимних разлечение...
2 - Составьте словосочетания со словами: иждивенец, вентилятор, компостировать,...
2 - используя дополнительный источник информации подготовте сообщение...
1 - Составить предложение со словами йогурт кусок угощайтесь вкусный...
3 - За 5 м ткани заплатили на 2400 р .60 к .больше чем за 2 м такой...
2 - Tom asked jane where on holiday. she goes b. will she go c. would...
1 - Решить примеры 156: 26,216: 54,2924: 68,3456: 72,29736: 56,38232:...
3
Расуждаем так. Обозначим n - количество использованных двоек. Если бы мистер Фокс использовал n=1 двойку, то получил бы число 3. При n=2 получаем 7, и т.д. Запишем в столбик:
Замечаем, что
То есть при n=2017 выражение будет равно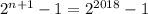
В двоичном виде число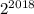 - это единица и 2018 нулей. Если вычесть из такого числа единицу, получим число, состоящее из 2018 единиц.
- это единица и 2018 нулей. Если вычесть из такого числа единицу, получим число, состоящее из 2018 единиц.
ответ: 2018