Преобразуйте формулы: a) F= X v Y v XY vY v XY, (просмотр картинки снизу для точного условия)
b) W =XYZ¯¯¯ v XY v (YZ¯ v XYZ ) v XZ
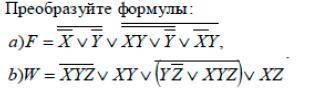
Другие вопросы по теме Информатика
Популярные вопросы
- Який вплив людина задає на атмосферу? Дайте відповідь будь ласка, дуже потрібно,тему...
3 - Найдите значение выражения...
2 - Друга сторона трикутника на 9 см більша, ніж перша, а третя в 2 рази більша...
1 - Скільки чисел у натуральному ряду від 35 до 100 та між 35 до 100...
3 - Написать структурные формулы следующих соединений: 3-бром-2-хлорпентана;...
2 - Ctg^2 x-cos^2 x=ctg^2 x*cos^2 x решите тождество ...
3 - Почему окруженцев, т.е. солдат, вырвавшихся из окружения, писатель назвал...
2 - Ребята решить, за решение....
3 - План до твору тореадори з васюківки 3 частина Як це все почалось( 1 роздiл...
1 - Найти вторую производную y=x^5-7x^3+3...
3
a) Нам дана формула F = X v Y v XY v Y v XY. Начнём пошагово преобразовывать её.
1. Внимательно посмотрев на формулу, мы замечаем, что Y встречается два раза рядом друг с другом: Y v Y. Это можно упростить до просто Y, так как объединение одинаковых переменных через ИЛИ даёт просто переменную саму по себе.
Получаем: F = X v Y v XY v XY.
2. Теперь замечаем, что XY v XY также повторяется два раза. Снова объединяем их, получаем просто XY.
Получаем: F = X v Y v XY.
3. На этом шаге у нас осталось только три переменных: X, Y и XY. Давайте объединим их.
Получаем: F = X v Y v XY.
Таким образом, мы преобразовали формулу F = X v Y v XY v Y v XY до простейшего вида F = X v Y v XY.
b) Теперь рассмотрим формулу W = XYZ¯¯¯ v XY v (YZ¯ v XYZ ) v XZ. Проанализируем каждую часть по отдельности.
1. Давайте начнём с разбора выражения XYZ¯¯¯. В данном случае, символ ¯ означает отрицание переменной Z. Таким образом, формула XYZ¯¯¯ означает, что переменные X, Y и Z отрицательны одновременно. Мы можем записать это так: XYZ.
2. В следующем выражении YZ¯, опять означает, что обе переменные Y и Z отрицательны одновременно.
3. XYZ обозначает, что все переменные X, Y и Z положительны одновременно.
4. Теперь давайте посмотрим на формулу внутри скобок: YZ¯ v XYZ. Здесь у нас ИЛИ объединяет два выражения: YZ¯ и XYZ.
5. Посмотрим теперь на всю формулу W = XYZ¯¯¯ v XY v (YZ¯ v XYZ ) v XZ. Мы можем записать это так: W = XYZ v XY v (YZ¯ v XYZ ) v XZ.
6. Теперь объединим выражение YZ¯ v XYZ с XYZ, так как они содержат одну и ту же переменную XYZ.
Получаем: W = XYZ v XY v XYZ v XZ.
7. На этом этапе у нас есть два одинаковых выражения, которые можно объединить.
Получаем: W = XYZ v XY v XZ.
Таким образом, мы преобразовали формулу W = XYZ¯¯¯ v XY v (YZ¯ v XYZ ) v XZ до простейшего вида W = XYZ v XY v XZ.
Надеюсь, ответ был понятным! Если вы имеете дополнительные вопросы, пожалуйста, сообщите мне!