Постройте алгоритм решения системы уравнений при изменяющимся значение икс от двух до 15 шагом 0,5
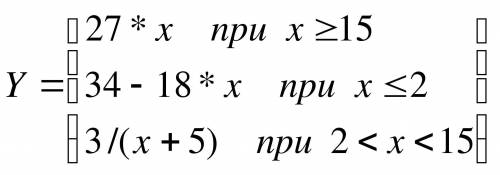
Другие вопросы по теме Информатика
Популярные вопросы
- Мастер и его ученик 3 часа вытачивали детали.мастер все это время работал...
3 - Спробуйте написати сценарій про надання невідкладної потерпілому, який отруївся...
3 - Подчеркни пропущенную орфограмму лебедь ( ) глазками( ) лапками ( ) гибкая(...
2 - Из семи дней недели было 3 солнечных дня. какую часть недели составляют...
1 - Украя пропасти давление 754 мм.чему равно атмосферное давление на её дне...
2 - Известно, что вектор |a| =2, вектор |b|=2, а косинус угла между векторами...
2 - Найдите площадь круг,если 4/9 длины окружности этого круга равны 49,6 см.(число...
1 - 1)почему за обедом полезно съедать сначала суп или салат? 2)почему необходимо...
3 - Явопрос по языку смотрите есть слова nine и что дальше по дан пример one...
3 - Отзыв о путешествие алисы к. булычёв...
1
1. Начнем с приведения системы уравнений к более простому виду, чтобы упростить решение. Для этого умножим первое уравнение на 2 и получим:
2x - y = 4
Теперь мы можем использовать метод подстановки.
2. Пусть x будет равно первому значению из данного диапазона, то есть 2. Тогда, подставляя это значение в первое уравнение, получим:
2 * 2 - y = 4
Упрощая это уравнение, получим:
4 - y = 4
Избавимся от константы, вычтя 4 с обеих сторон:
-y = 0
Таким образом, получаем:
y = 0
Значит, первое решение системы уравнений будет (x = 2, y = 0).
3. Теперь, используя второе уравнение, найдем значение y при данном x:
-x + y = 3
Подставляем первое значение x = 2:
-2 + y = 3
Найдем значение y, сложив 2 с обеих сторон:
y = 5
Значит, второе решение системы уравнений будет (x = 2, y = 5).
4. Продолжаем этот процесс для остальных значений x из данного диапазона (от 2 до 15 с шагом 0,5). После каждой итерации получаем пары значений (x, y), которые являются решениями системы уравнений.
Для примера:
- При x = 2.5 получим (x = 2.5, y = 5.5).
- При x = 3 получим (x = 3, y = 6).
- При x = 3.5 получим (x = 3.5, y = 6.5).
- И так далее, пока не достигнем x = 15.
5. Записываем все полученные пары значений (x, y) в виде таблицы или графика, чтобы визуально представить решения системы уравнений для изменяющихся значений x от 2 до 15 с шагом 0,5.
Надеюсь, этот алгоритм поможет вам решить данную систему уравнений и позволит лучше понять процесс решения.