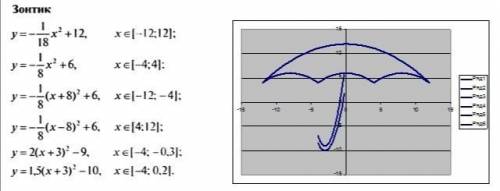
Построить график функций в одной системе координат чтобы получился зонтик

Для построения графика функций и получения зонтика в одной системе координат, нам понадобится разбить конструкцию зонтика на отдельные функции, которые будут соответствовать отдельным частям зонтика.

1. Верхняя часть зонта:
Из графика видно, что верхняя часть зонта имеет форму половины эллипса. Для построения этой функции, мы можем использовать уравнение эллипса в общем виде: (x-h)^2/a^2 + (y-k)^2/b^2 = 1, где (h,k) - координаты центра эллипса, а a и b - полуоси эллипса.
Видно, что по оси x у эллипса проходит вертикальная симметрия, поэтому будем строить только положительную часть эллипса.
В данном случае, координаты центра (h,k) примерно равны (2,3), полуось a - около 2, а полуось b - около 3. Теперь можем составить уравнение нашего эллипса:
(x-2)^2/2^2 + (y-3)^2/3^2 = 1.

2. Правая часть зонта:
Эта часть зонта имеет форму прямой линии, которая идет вниз. Уравнение прямой линии имеет вид y = kx + b, где k - угловой коэффициент прямой, а b - коэффициент сдвига по y.
В данном случае прямая идет под углом, поэтому её угловой коэффициент будет зависеть от тангенса угла наклона прямой. Также нам нужно знать координаты двух точек, через которые проходит прямая, чтобы знать её положение.
Исходя из графика, мы видим, что прямая проходит через точки (6,3) и (6,-3).
Теперь можем составить уравнение нашей прямой:
y = (3-(-3))/(6-6) * x + b,
то есть y = 0 * x + b,
то есть y = b.

3. Левая часть зонта:
Эта часть зонта также имеет форму прямой линии, которая идет вниз. По аналогии с правой частью, можем использовать уравнение прямой линии y = kx + b.
Также мы видим, что прямая проходит через точки (-6,3) и (-6,-3).
Теперь можем составить уравнение:
y = (3-(-3))/(-6-(-6)) * x + b,
то есть y = 0 * x + b,
то есть y = b.

4. Нижняя часть зонта:
Также для нижней части зонта можем применить уравнение эллипса, аналогично верхней части. Поскольку это половина эллипса, мы будем рассматривать только нижнюю половину, где y < 0.
Видно, что по оси x проходит вертикальная симметрия, и также получаем:
(x-2)^2/2^2 + (y+3)^2/3^2 = 1.

Теперь можно построить график всех функций в одной системе координат.
Воспользуйтесь программами для построения графиков, такими как GeoGebra или Excel, чтобы визуализировать полученные уравнения.
На получившемся графике вы увидите зонтик, построенный из соединенных функций - верхнюю и нижнюю половины эллипсов, а также правую и левую прямые, как показано на изначальном изображении.