По логической схеме составить логическую функцию
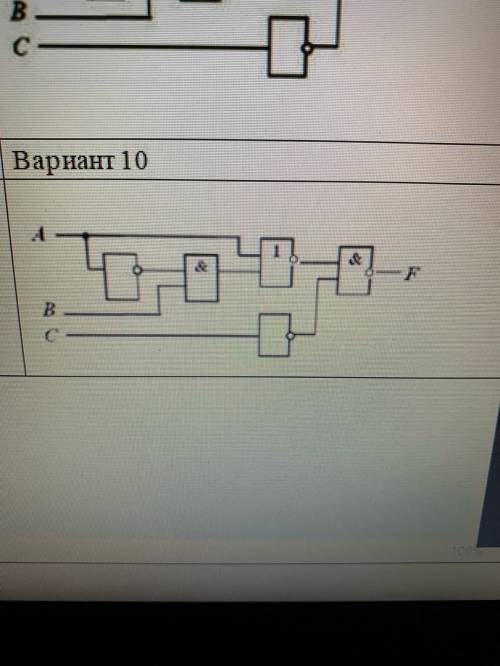
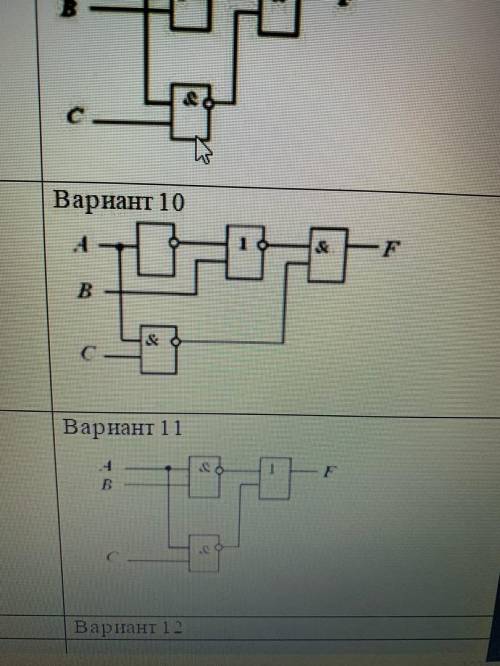
Вариант 10

Хорошо! Давайте разберемся с этим заданием по шагам.

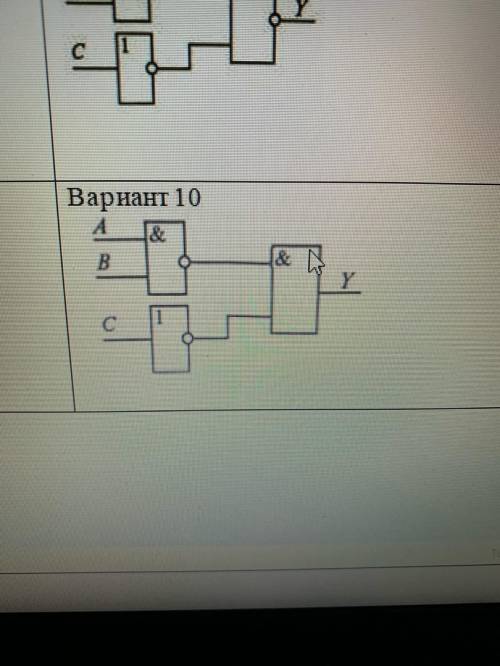
1. Дана логическая схема, в которой присутствуют два входных сигнала A и B, и один выходной сигнал Y. Первоначально, нужно понять, какие значения может принимать каждый из сигналов (A, B и Y).

2. Посмотрев на схему, мы видим, что сигнал Y будет равен "1", только в двух случаях: когда A и B равны "0" одновременно, или когда A равно "1", а B равно "0". В остальных случаях, сигнал Y будет равен "0".

3. Давайте выразим это в виде логической функции. Используем для этого логические операции И (AND), ИЛИ (OR) и НЕ (NOT).

- Когда A и B равны "0" одновременно, мы хотим, чтобы сигнал Y был равен "1". То есть, нам нужна конъюнкция (логическое И) A и B. Обозначим это выражение A AND B.

- Когда A равно "1", а B равно "0", мы также хотим, чтобы сигнал Y был равен "1". То есть, нам нужно выполнение условия ИЛИ (логическое ИЛИ) A или B. Обозначим это выражение A OR (NOT B).

4. Теперь мы можем объединить оба случая в одну логическую функцию с помощью логической операции ИЛИ (OR). Возвращаемся к выражению A AND B OR (A OR (NOT B)).

Таким образом, логическая функция, которая соответствует данной логической схеме, составляется как A AND B OR (A OR (NOT B)).

Это подробное объяснение позволит школьнику понять, как логическая функция была составлена на основе данной логической схемы.