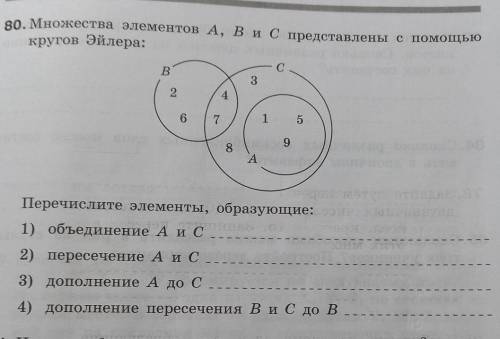
надо перечислить элементы, образующие:
1) объединение А и С
2) пересечение А и С
3) дополнение А до С
4) дополнение пересечения В и С до В​

Для того чтобы ответить на этот вопрос, нам необходимо знать значения множеств A, B и C, представленных на диаграмме Эйлера.

1) Объединение А и С (A ∪ C) означает, что мы должны объединить все элементы, содержащиеся в множестве A и все элементы, содержащиеся в множестве C. Наша задача - найти все элементы, которые есть в А или C или в обоих множествах одновременно.

- В множестве А присутствуют элементы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
- В множестве С присутствуют элементы: 3, 4, 5, 11, 12, 13, 14, 15.

Чтобы найти объединение А и С, нам нужно просто объединить все элементы, которые есть в обоих множествах. Поэтому, объединение А и С равно 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15.

2) Пересечение А и С (A ∩ C) означает, что мы должны найти все элементы, присутствующие в обоих множествах одновременно - т.е. элементы, которые пересекаются.

- В множестве А присутствуют элементы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
- В множестве С присутствуют элементы: 3, 4, 5, 11, 12, 13, 14, 15.

Мы должны найти элементы, которые есть и в А, и в С. Поэтому пересечение А и С равно 3, 4, 5.

3) Дополнение А до С (C \ A) означает, что мы должны найти все элементы, которые находятся в множестве С, но не находятся в множестве А.

- В множестве А присутствуют элементы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
- В множестве С присутствуют элементы: 3, 4, 5, 11, 12, 13, 14, 15.

Чтобы найти дополнение А до С, нам нужно исключить все элементы, которые есть в А из множества С. Поэтому дополнение А до С равно 11, 12, 13, 14, 15.

4) Дополнение пересечения B и С до В (B ∩ C)' означает, что мы должны найти все элементы, которые находятся в множестве В, но не пересекаются с множеством С.

- В множестве B присутствуют элементы: 4, 5, 6, 7, 15.
- В множестве С присутствуют элементы: 3, 4, 5, 11, 12, 13, 14, 15.

Мы должны найти элементы, которые есть в B, но не пересекаются с С. Поэтому дополнение пересечения В и С до В равно 6, 7.

Надеюсь, эти подробности помогут вам понять, как получить элементы, образующие объединение А и С, пересечение А и С, дополнение А до С и дополнение пересечения В и С до В.