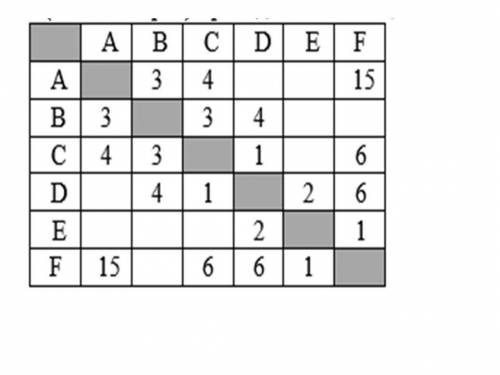
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых (в километрах) приведена в таблице. Определите длину кратчайшего пути между пунктами A и E, проходящего через пункт С. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.

Чтобы определить длину кратчайшего пути между пунктами A и E, проходящего через пункт C, мы можем использовать алгоритм Дейкстры.

Шаг 1: Создайте граф из данной таблицы. Каждый населенный пункт будет представлен узлом, а дороги - ребрами. Узлы A, B, C, D, E, F будут соответствовать населенным пунктам, а вес каждого ребра будет соответствовать протяженности дороги.

Шаг 2: Назначьте начальное значение расстояния для каждого узла. Начальные расстояния для всех узлов, кроме A, будут бесконечность. Начальное расстояние для узла A будет 0.

Шаг 3: Отметьте узел A как посещенный.

Шаг 4: Для каждого соседнего узла B с A обновите его расстояние от начального узла A. Если новое расстояние меньше текущего расстояния, то обновите значение расстояния.

Шаг 5: Отметьте текущий узел как посещенный. Выберите узел с наименьшим расстоянием от начального узла из непосещенных узлов и перейдите к шагу 4.

Шаг 6: Повторите шаги 3-5, пока все узлы не будут посещены или пока все узлы, кроме целевого узла (E), не будут иметь бесконечную длину пути.

Шаг 7: Используя обратное движение от E к A, выберите кратчайший путь, проходящий через C, и определите его длину.

Решение:

Шаг 1: Создаем граф с узлами A, B, C, D, E, F и ребрами, между которыми указаны соответствующие значения протяженности дороги.

Шаг 2: Начальное значение расстояния устанавливаем в бесконечность для всех узлов, кроме A. Начальное расстояние для узла A будет 0.

Шаг 3: Отмечаем узел A как посещенный.

Шаг 4: Обновляем расстояние от начального узла A до каждого смежного узла B. Если новое расстояние меньше текущего расстояния, обновляем значение расстояния.

- Расстояние от A до B равно 6 (текущее значение).
- Расстояние от A до C равно 4 (текущее значение).
- Расстояние от A до D равно бесконечности (текущее значение).
- Расстояние от A до F равно бесконечности (текущее значение).

Шаг 5: Помечаем узел A как посещенный и выбираем узел с наименьшим расстоянием от начального узла из непосещенных узлов. В данном случае это узел C.

Шаг 4 (продолжение): Обновляем расстояние от начального узла A до каждого смежного узла B, через узел C.

- Расстояние от A до B через C равно 6 (текущее значение).
- Расстояние от A до D через C равно 5 (текущее значение).
- Расстояние от A до F через C равно бесконечности (текущее значение).

Шаг 5 (продолжение): Помечаем узел C как посещенный и выбираем узел с наименьшим расстоянием от начального узла из непосещенных узлов. В данном случае это узел D.

Шаг 4 (продолжение): Обновляем расстояние от начального узла A до каждого смежного узла B, через узлы C и D.

- Расстояние от A до B через C и D равно 6 (текущее значение).
- Расстояние от A до F через C и D равно 10 (текущее значение).

Шаг 5 (продолжение): Помечаем узел D как посещенный и выбираем узел с наименьшим расстоянием от начального узла из непосещенных узлов. В данном случае это узел B.

Шаг 4 (продолжение): Обновляем расстояние от начального узла A до каждого смежного узла B, через узлы C, D и B.

- Расстояние от A до F через C, D и B равно 10 (текущее значение).

Шаг 5 (продолжение): Помечаем узел B как посещенный и выбираем узел с наименьшим расстоянием от начального узла из непосещенных узлов. В данном случае это узел F.

Шаг 4 (продолжение): Обновляем расстояние от начального узла A до узла F.

- Расстояние от A до F через C, D и B равно 10 (текущее значение).

Шаг 5 (продолжение): Помечаем узел F как посещенный. Все узлы посещены, за исключением узла E.

Шаг 6: Используя обратное движение от E до A, находим кратчайший путь, проходящий через C. Путь будет выглядеть так: A -> C -> D -> B -> F -> E.

Шаг 7: Определяем длину кратчайшего пути: 4 + 1 + 2 + 3 + 2 = 12.

Итак, длина кратчайшего пути между пунктами A и E, проходящего через пункт C, составляет 12 километров.