Логические функции
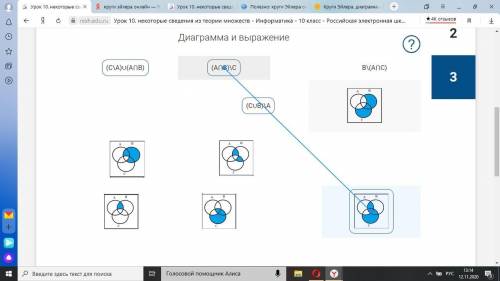
Диаграмма и выражение

(C\A)∪(A⋂B)
(A⋂B)\C
B\(A⋂C)
(C∪B)\A

Для решения данной задачи по логическим функциям, нужно разобрать каждое выражение по очереди, используя операции объединения (обозначается символом ∪), пересечения (обозначается символом ⋂) и разности (обозначается символом \). 1) (C\A)∪(A⋂B) Сначала нужно рассмотреть (C\A), что означает элементы, которые принадлежат множеству C, но не принадлежат множеству A. Затем нужно объединить это множество с пересечением множеств A и B. Чтобы понять это графически, нужно построить диаграмму по множеству. Посмотрите на изображение внизу.  Слева представлено множество C, справа множество A. Пустые круги символизируют элементы, которые не принадлежат каждому из множеств. Заполненные круги символизируют элементы, которые принадлежат каждому из множеств. Таким образом, (C\A) означает элементы, которые принадлежат множеству C, но не принадлежат множеству A. Это представлено на диаграмме слева в виде пустого круга, но заполненного круга (символизирующего множество C). Затем, рассмотрим пересечение множеств A и B, обозначенное A⋂B. Это означает элементы, которые принадлежат как множеству A, так и множеству B. Это представлено на диаграмме справа в виде двух смежных заполненных кругов (символизирующих множества A и B) с перекрестными участками. Теперь, чтобы получить ответ на выражение (C\A)∪(A⋂B), нужно объединить все элементы из множества (C\A) и множества (A⋂B). Для этого нужно использовать объединение (∪). Результат будет принадлежать любому из этих множеств. Другой способ решения такой, что необходимо использовать основные свойства логических функций. Для выражения (C\A)∪(A⋂B) может быть использован закон де Моргана, который гласит: A∪B = A'\B', где A' и B' - это дополнения A и B соответственно. В этом случае, можно записать выражение в виде (C\A)∪(A⋂B) = ((C'\A')⋂(A\B)). После этого, можно дать пояснение о дополнениях и пересечении множеств A и B, соответственно. 2) (A⋂B)\C Это означает элементы, которые принадлежат как множествам A и B, но не принадлежат множеству C. Графически, это представлено на диаграмме в виде пересечения множеств A и B (два смежных заполненных круга) без участка, принадлежащего множеству C(пустой круг). 3) B\(A⋂C) Это означает элементы, которые принадлежат множеству B, но не принадлежат пересечению множеств A и C. Графически, это представлено на диаграмме в виде множества B (пустой круг) с пустым участком в области пересечения множеств A и C (два пересекающихся пустых круга). 4) (C∪B)\A Это означает элементы, которые принадлежат объединению множеств C и B, но не принадлежат множеству A. Графически, это представлено на диаграмме в виде объединения множеств C и B (пустой и заполненный круги) без участка, принадлежащего множеству A (пустой круг). Надеюсь, что данное объяснение помогло вам понять решение задачи по логическим функциям. Если у вас есть еще вопросы, пожалуйста, не стесняйтесь задавать.