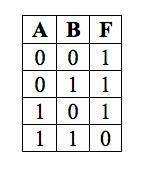
Какому логическому выражению соответствует таблица истинности (фото) AvB
AvB (черточка над А)
A^B
A^B (черточка над всем выражением)

Давайте разберемся с этим вопросом. Для начала, давайте определим, что означает каждый из логических операторов, которые встречаются в вашем вопросе:

1. А - это первое выражение или условие.
2. В - это второе выражение или условие.

Теперь, давайте разберемся с каждым из логических выражений по очереди:

1. AvB - это логическое ИЛИ между выражением А и выражением В. Если хотя бы одно из условий (А или В) истинно, то все выражение будет истинно.

2. AvB (черточка над А) - это тоже самое, что и предыдущее выражение, только с отрицанием А. То есть, если А ложно, а В истинно, то все выражение будет истинно.

3. A^B - это логическое И между выражением А и выражением В. Выражение будет истинным, только если оба условия (А и В) истинны одновременно.

4. A^B (черточка над всем выражением) - это тоже самое, что и предыдущее выражение, только с отрицанием всего выражения. То есть, если А и В одновременно ложны, или хотя бы одно из условий истинно, то все выражение будет ложно.

Теперь перейдем к таблице истинности, чтобы определить, какому логическому выражению она соответствует.

В таблице истинности, которую вы приложили, есть два столбца для переменных А и В, а также столбцы для каждого из логических выражений. Для каждой комбинации значений переменных А и В в таблице, укажите, истинно или ложно выражение, соответствующее этой комбинации.

Посмотрим на каждое выражение по отдельности:

1. AvB (черточка над А) - из таблицы, видно, что выражение истинно только для комбинации, когда А ложно, а В истинно.

2. AvB - из таблицы видно, что выражение истинно для всех комбинаций, где либо А, либо В (или оба) истинны.

3. A^B - из таблицы, видно, что выражение истинно только для комбинации, когда и А, и В истинны.

4. A^B (черточка над всем выражением) - из таблицы видно, что выражение истинно для всех комбинаций, где одно или оба условия (А и В) истинны, и ложно только в том случае, когда А и В оба ложны.

Таким образом, можно сказать, что таблица истинности соответствует следующим логическим выражениям:

1. AvB (черточка над А) - истинно только для комбинации, когда А ложно, а В истинно.
2. AvB - истинно для всех комбинаций, где либо А, либо В (или оба) истинны.
3. A^B - истинно только для комбинации, когда и А, и В истинны.
4. A^B (черточка над всем выражением) - истинно для всех комбинаций, где одно или оба условия (А и В) истинны, и ложно только в том случае, когда А и В оба ложны.