Для заданного логического выражения: 1) Построить таблицу истинности;
2) Упростить высказывания, используя законы алгебры логики;
3) Полученный результат проверить, построив для него таблицу истинности.
ОЧЕНЬ
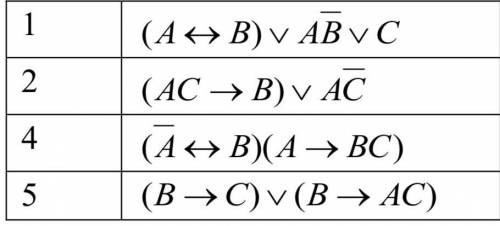
Другие вопросы по теме Информатика
Популярные вопросы
- Какое расстояние пролетпет самолёт за 1 мин. если он летит со скоростью...
1 - Почему возникла феодальная раздробленность в западной европе дата...
3 - Продолжите и запишите цепочки слов-ассоциаций 1.моряк - капитан,...
3 - Как правильно написать : мы ведем репортаж со владимировской области...
2 - Какие океаны омывают берега африки и австралии...
3 - 16)5*(9х-10)=40 17)31=111-х-7х 18)1,7(13+3х)-0,3=1,4 19)0=15+х-8х-3х-6х+х...
3 - Надо изменить место ударение и записать парами должно получится новое...
2 - Что такое сравнительный оборот? только желательно кратко...
1 - Напишите 15 слов на приставку полу и 15 на пол...
2 - Всемирное население в россии, творение человека...
3
1) Построим таблицу истинности для заданного логического выражения.
Для этого нам нужно выписать все возможные комбинации значений переменных (A и B) и вычислить значение выражения для каждой комбинации. В данном случае у нас есть две переменных, поэтому возможны четыре комбинации:
- При A = 0 и B = 0:
Выражение (A ∨ B) ∧ (¬A) будет равно (0 ∨ 0) ∧ (¬0) = 0 ∧ 1 = 0
- При A = 0 и B = 1:
Выражение (A ∨ B) ∧ (¬A) будет равно (0 ∨ 1) ∧ (¬0) = 1 ∧ 1 = 1
- При A = 1 и B = 0:
Выражение (A ∨ B) ∧ (¬A) будет равно (1 ∨ 0) ∧ (¬1) = 1 ∧ 0 = 0
- При A = 1 и B = 1:
Выражение (A ∨ B) ∧ (¬A) будет равно (1 ∨ 1) ∧ (¬1) = 1 ∧ 0 = 0
Таким образом, таблица истинности для заданного выражения выглядит следующим образом:
| A | B | (A ∨ B) ∧ (¬A) |
|---|---|---------------|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
2) Теперь упростим высказывание, используя законы алгебры логики.
Для упрощения выражения можно использовать различные законы алгебры логики, такие как ассоциативный, коммутативный и дистрибутивный законы, а также законы двойного отрицания и идемпотентности.
При анализе выражения (A ∨ B) ∧ (¬A) можно заметить, что закон идемпотентности позволяет нам упростить это выражение до (A ∨ B) ∧ (¬A), так как (A ∨ B) ∨ (¬A) равно (A ∨ B) при любом значении A.
3) Проверим полученный результат, построив для него таблицу истинности.
| A | B | (A ∨ B) ∧ (¬A) | (A ∨ B) |
|---|---|---------------|---------|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 |
Как видно из таблицы истинности, значения выражения (A ∨ B) ∧ (¬A) совпадают с значениями выражения (A ∨ B), что подтверждает правильность упрощения.
Таким образом, исходное выражение (A ∨ B) ∧ (¬A) упростили до (A ∨ B) с помощью закона идемпотентности, и это упрощенное выражение подтверждается таблицей истинности.