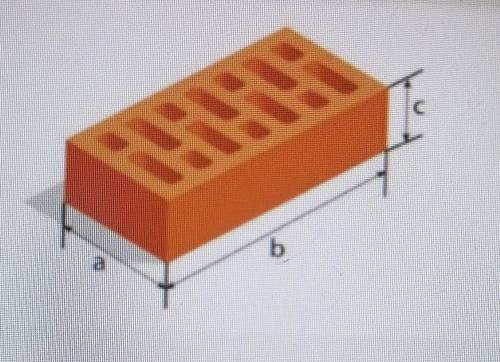
Даны значение ширины длины и высоты кирпича а, b, c. Найди соотношение объема кирпича к площади
полной поверхности (рис. 2)
В python
​

Для решения данной задачи, нам необходимо найти объем кирпича и площадь его полной поверхности. Объем кирпича можно найти, умножив его длину, ширину и высоту. То есть: V = a * b * c Площадь полной поверхности кирпича можно найти, сложив площади всех его граней. В данном случае, у кирпича есть 6 граней (4 боковые грани, верхняя и нижняя грани). Площадь каждой грани равна произведению длины на ширину. То есть: S = 2(ab + ac + bc) Итак, у нас есть формулы для вычисления объема и площади полной поверхности. Теперь мы можем приступить к решению задачи. 1. Сперва, нужно объявить значения ширины (a), длины (b) и высоты (c) кирпича в программе, а также определить некоторые вспомогательные переменные для хранения результатов: a = 5 b = 7 c = 10 2. Затем, по формуле вычисляем объем: V = a * b * c 3. Теперь по формуле вычисляем площадь полной поверхности: S = 2 * (a*b + a*c + b*c) 4. Далее, находим соотношение объема кирпича к площади полной поверхности: ratio = V / S 5. Выводим результаты на экран: print("Объем кирпича:", V) print("Площадь полной поверхности:", S) print("Соотношение объема кирпича к площади:", ratio) Теперь, если мы запустим программу, то получим ответ в виде объема кирпича, площади полной поверхности и соотношения объема к площади. Например, для значений a=5, b=7 и c=10, мы получим следующий вывод: Объем кирпича: 350 Площадь полной поверхности: 410 Соотношение объема кирпича к площади: 0.8536585365853658 Таким образом, соотношение объема кирпича к площади полной поверхности составляет примерно 0.854.