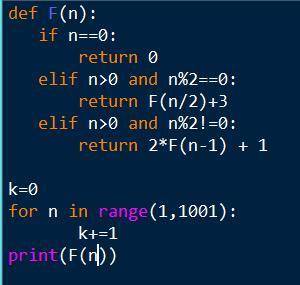
Алгоритм вычисления значения функции F(n), где n – целое число, задан следующими соотношениями: F(0) = 0
F(n) = F(n/2) + 3, при чётном n > 0
F(n) = 2·F(n - 1) + 1, при нечётном n > 0
Сколько различных значений может принимать функция F(n) при n, принадлежащих отрезку [1; 1000]?
Другие вопросы по теме Информатика
Популярные вопросы
- Заповніть пропуски емфатичними (підсилювальними) займенниками....
2 - «Как в рассказе И. А. Солженицына «Один день Ивана Денисовича»...
1 - Найдите сумму геометрической прогрессии (bn), если: b1=1, q=0,6....
1 - У меня подключены наушники в передний переходники, звук есть но...
3 - Середня солоність поверхневих вод тихого океану...
2 - Во по Химии. С какими из предложенных веществ будет реагировать...
1 - объяснить, почему так объяснить, почему так...
2 - Обчисліть масу кальцій карбонату, що утворюеться внаслідок взаемодії...
3 - Мне надо писать сочинение на тему Мое село на немецком...
3 - Какие гены у человека наследуются сцепленно с полом?...
3
Да, все правильно, ровно 1000 значений, ведь они соответствуют условию n>0
aboba=[]
def F(n):
global aboba
if n==0:
return 0
elif n>0 and n%2==0:
return F(n/2)+3
elif n>0 and n%2==1:
return 2*F(n-1)+1
count=0
for i in range(1,1001):
aboba.append(F(i))
print(len(set(aboba)))