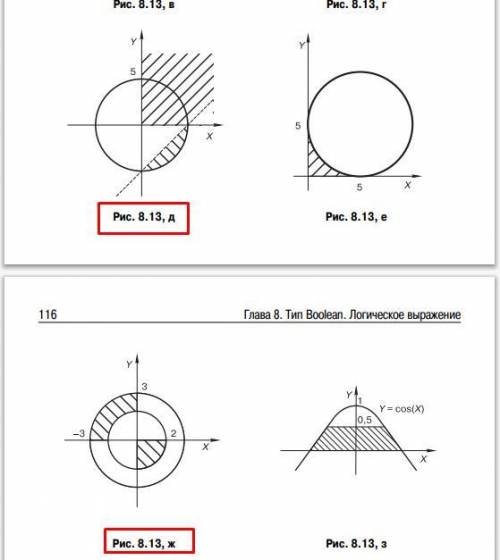
8.8. Записать на Паскале логическое выражение, зависящее от X и Y, которое принимает значение True, если точка с координатами (X, Y)
принадлежит закрашенной области, и False, если не принадлежит
(рис. 8.13, а–м). Границы, которые принадлежат области, проведены
сплошной линией, а те, которые не принадлежат, — пунктирной.

Чтобы решить эту задачу на Паскале, мы можем использовать следующий алгоритм:

1. Определить границы области, принадлежащей закрашенной области. Мы видим, что у нас есть две секции - секция A и секция B.

2. Для секции A, границами области будут линии y = x и y = -x. Мы можем записать логическое условие для этой секции:
((x >= -4) and (x <= 4) and (y >= -x) and (y >= x)) or ((x > 4) and (x <= 10) and (y >= (x - 8)) and (y >= (-x + 8)))

Объяснение: Мы проверяем, находятся ли координаты точки (X, Y) внутри границ секции A. Первые два условия (x >= -4) и (x <= 4) проверяют, что X находится в пределах от -4 до 4. Следующие два условия (y >= -x) и (y >= x) проверяют, что Y больше или равно значениям -X и X соответственно. Последние два условия (x > 4) и (x <= 10) проверяют, что X находится в диапазоне от 4 до 10 включительно.
Затем два условия (y >= (x - 8)) и (y >= (-x + 8)) проверяют, что Y больше или равно значениям функций y = x - 8 и y = -x + 8, соответственно.

3. Для секции B, границами области будут линии y = -2 и y = 2. Мы можем записать логическое условие для этой секции:
(x > -10) and (x < -4) and (y >= -2) and (y <= 2)

Объяснение: Мы проверяем, находятся ли координаты точки (X, Y) внутри границ секции B. Условия (x > -10) и (x < -4) проверяют, что X находится в диапазоне от -10 до -4. Условия (y >= -2) и (y <= 2) проверяют, что Y находится в диапазоне от -2 до 2 включительно.

4. Итак, чтобы записать логическое выражение, которое принимает значение True, если точка с координатами (X, Y) принадлежит закрашенной области, и False, если не принадлежит, мы комбинируем условия для обеих секций с оператором "or":
(((x >= -4) and (x <= 4) and (y >= -x) and (y >= x)) or ((x > 4) and (x <= 10) and (y >= (x - 8)) and (y >= (-x + 8)))) or ((x > -10) and (x < -4) and (y >= -2) and (y <= 2))

Объяснение: Это логическое выражение проверяет, находятся ли координаты точки (X, Y) внутри закрашенных границ обеих секций A и B.

Надеюсь, это решение поможет вам понять, как записать логическое выражение на Паскале для данной задачи. Если у вас возникнут дополнительные вопросы, не стесняйтесь задавать их. Удачи вам!