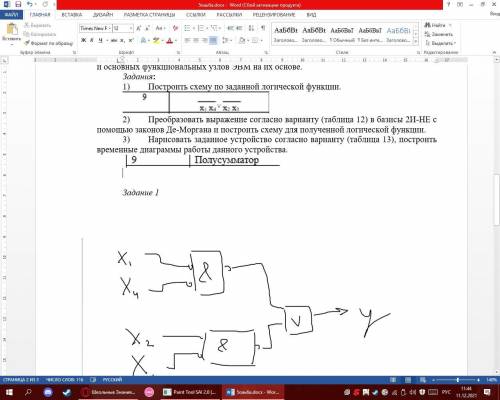
1) Построить схему по заданной логической функции. 2) Преобразовать выражение в базисы 2И-НЕ с законов Де-Моргана и построить схему для полученной логической функции.
Другие вопросы по теме Информатика
Популярные вопросы
- 3. Вероятность брака на заводе равняется 0,2. Сколько бракованных...
3 - Почему стоит запятая в предложениях: 1.С брошенных зимних дорог...
2 - В молекуле днк тиминовые нуклеотиды составляют 32%. Определите...
1 - Поділити 100 грн. пропорційні до чисел 2, 3, 5....
1 - В игре полезные ресурсы генерируются с вероятность 0,34 для клетки....
1 - Дуже треба дам всьо що є. Напишіть твір мініатюру на тему (на...
1 - Характеристика головного героя твору іловайськ (розповідь коли...
2 - Рівнобедрений трикутник, бічна сторона якого дорівнює 6, а кутпри...
2 - Укажіть ряд формул речовин несолетворних оксидів? Дайте правильну...
2 - 1 После шипящих под ударением в суффиксах имен существительных...
1
1) Схема по заданной логической функции:
Для начала определим, какие переменные участвуют в данной функции. Нам дано выражение F = (A AND B) OR (C NOR D), где A, B, C и D - переменные.
Составим таблицу истинности для заданной логической функции:
| A | B | C | D | F |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | ? |
| 0 | 0 | 0 | 1 | ? |
| 0 | 0 | 1 | 0 | ? |
| 0 | 0 | 1 | 1 | ? |
| 0 | 1 | 0 | 0 | ? |
| 0 | 1 | 0 | 1 | ? |
| 0 | 1 | 1 | 0 | ? |
| 0 | 1 | 1 | 1 | ? |
| 1 | 0 | 0 | 0 | ? |
| 1 | 0 | 0 | 1 | ? |
| 1 | 0 | 1 | 0 | ? |
| 1 | 0 | 1 | 1 | ? |
| 1 | 1 | 0 | 0 | ? |
| 1 | 1 | 0 | 1 | ? |
| 1 | 1 | 1 | 0 | ? |
| 1 | 1 | 1 | 1 | ? |
Здесь ? обозначает неизвестное значение функции F при данных значениях переменных. Заполним таблицу истинности значениями функции F.
| A | B | C | D | F |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Теперь мы можем построить схему по этой таблице. Для этого нам понадобятся элементы логических схем, такие как И (AND), НЕ (NOT), ИЛИ (OR), NOR.
Схема для заданной логической функции будет выглядеть следующим образом:
2) Преобразование выражения в базисы 2И-НЕ с использованием законов Де-Моргана и построение схемы для полученной логической функции:
Перейдем к преобразованию выражения в базисы 2И-НЕ с помощью законов Де-Моргана.
Исходное выражение: F = (A AND B) OR (C NOR D)
1. Применим закон Де-Моргана к операции ИЛИ (OR):
F = NOT(NOT((A AND B) OR (C NOR D)))
2. Применим закон Де-Моргана к операции НЕ (NOT):
F = NOT(NOT(A AND B) AND NOT(C NOR D))
3. Применим закон Де-Моргана к операции И (AND):
F = NOT((NOT A OR NOT B) AND NOT(NOT C AND D))
4. Применим закон Де-Моргана к операции НЕ (NOT):
F = (NOT(NOT A OR NOT B)) OR (NOT(NOT C AND D))
Теперь мы можем построить схему для полученной логической функции.
Схема для преобразованной логической функции будет выглядеть следующим образом: