1. Геометрия
  2. Знайдіть сторони трикутника,

Знайдіть сторони трикутника, якщо вони відносяться один до одного як 25: 26: 3, а його площа 9см2

cako2004 cako2004    3   22.05.2019 13:20    2

Ответы
ОверДовн ОверДовн  01.10.2020 07:37

Пускай х-1 часть,тогда:
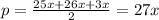
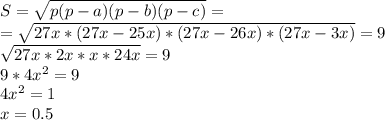
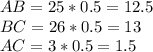
АВ=25х;ВС=26х;АС=3х
Выразим площадь тр-ка через теорему Герона,для этого найдем полупериметр:
p=\frac{25x+26x+3x}{2}=27x
Теперь записывает площадь:
S=\sqrt{p(p-a)(p-b)(p-c)}=\\=\sqrt{27x*(27x-25x)*(27x-26x)*(27x-3x)}=9\\\sqrt{27x*2x*x*24x}=9\\9*4x^2=9\\4x^2=1\\x=0.5
Теперь наши стороны:
AB=25*0.5=12.5\\BC=26*0.5=13\\AC=3*0.5=1.5

ПОКАЗАТЬ ОТВЕТЫ
Elizaveta30122005 Elizaveta30122005  01.10.2020 07:37

находим полупериметр (25х+26х+3х)\2 = 27х. теперь по теореме виетта подставляем данное значение и приравниваем к площади. То есть S=sqrt(27x*(27x-26x)*(27x-25x)*(27x-3x) = 9. отсюда x^2*36=9 отсюда X=3\6 отсюда находим стороны. A=25*(3\6)=75/6. B= 26 * (3/6) = 13 C= 3*(3/6) = 9/6

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
mlpfim2004 mlpfim2004  10.07.2019 18:10
35 две прямые пересекаются ,притом ,что сумма градусных мер трех образованным этим углам равняется 320 градусов . найдите угол между прямыми...
Sherstev Sherstev  07.06.2019 04:30
Втреугольнике abc угол c равен 90°,угол a равен 30°,ab=40. найдите bc...
26090204A 26090204A  07.06.2019 04:30
Кут між площинами рівностороннього трикутника авс і авd = 60 градусів. знайдіть відстань міжточками с і d, якщо аd = 2корінь з 3...
ШколоЛОх ШколоЛОх  21.05.2020 17:31
Яку роботу виконує електричний струм за 10хв на ділянці кола, якщо напруга на цій ділянці 36 В, а сила струму 0,5 А...
kalmuratov70 kalmuratov70  22.05.2020 17:48
1. Прямые m и n параллельны, угол 1 равен 36 градусов, угол 2 - 104 градуса. Укажите, чему равен угол 3. 2. Прямые а и b параллельны, с - секущая, угол 1 равен 124 градуса. Запишите,...
lada48 lada48  22.05.2020 17:49
Составьте общее уравнение прямой проходящей через точки А(2;6) и В(-4;0)....
valerea0 valerea0  24.01.2021 19:27
с геометрией С решение и рисунком...
krevisdons krevisdons  24.01.2021 19:27
Прямые А и Б паралельны. Найдите величину угла 2, если угол 1 - 63°...
олтисьл олтисьл  24.01.2021 19:30
решить геометрия восьмой класс с решением, а то Я совсем запутался( Задачи на подобие треугольников...
anelya033 anelya033  24.01.2021 19:30
Гіпотенуза прямокутного трикутника дорівнює 20 см, а біль- ший катет — 16 см. Знайдіть відрізки, на які серединний перпендикуляр гіпотенузи ділить більший катет....

Популярные вопросы