Знайдіть площу круга, вписаного в рівнобічну трапецію з основами 2 см і

18 см

Ответы

pepsy94zm 12.10.2020 05:51

Задача: Найти площадь окружности, вписанной в равностороннюю трапецию с основаниями 2 см и 18 см.

Площадь окружности: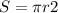 $S = \pi r2$

В трапецию можно вписать окружность в том случае, если суммы её противоположных сторон равны.

b+c = a+a, где b, c — основания трапеции, а — боковые стороны

Радиус вписанной в трапецию окружности равен половине высоты трапеции.

$r = \frac{h}{2} = \frac{\sqrt{bc} }{2}$ ,

где b, c — основания трапеции

$r = \frac{\sqrt{2\cdot 18} }{2} = \frac{\sqrt{36} }{2}=\frac{6}{2}=3 \:\:(cm)$

Подставим значения в формулу площади окружности:

$S = \pi r2\\S = \pi \cdot 3^2 = 9\pi \: \approx \: 28.27 \:\:(cm^2)$

ответ: Площадь окружности — 9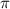 $\pi$ см², что приблизительно равно 28,27 см².

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

Galya03 05.12.2021 16:45

Cocos228 05.12.2021 16:49

ангел813 28.06.2019 04:50

Skyflay12367 28.06.2019 05:00

Adelina12005 28.06.2019 05:00

marychevakristi 28.06.2019 05:00

Нюйва 28.06.2019 05:00

KarakatitsaKrutitsa 28.06.2019 05:00

volk910 03.09.2019 13:20

Надо с рисунком в прямоугольном треугольнике авс (...

Mixachu 03.09.2019 13:20