1. Геометрия
  2. Знайдіть площу фігури

Знайдіть площу фігури , симетричної фігурі x^2-4x+y^2-6y=1 відносно початку координат
ів Найдите площадь внешней, симметричной действия x ^ 2-4x + y ^ 2-6y = 1 существенно заданный координат

mmedvedev389 mmedvedev389    1   08.05.2020 20:19    10

Ответы
Sn9 Sn9  14.10.2020 12:05

14\pi

Объяснение:

Преобразуем уравнение фигуры:

x^{2} - 4x + y^{2} - 6y = 1\\\\(x^{2} - 4x + 4) - 4 + (y^{2} - 6y + 9) - 9 = 1\\\\(x - 2)^{2} + (y - 3)^{2} - 13 = 1\\\\(x - 2)^{2} + (y - 3)^{2} = 14\\\\(x - 2)^{2} + (y - 3)^{2} = (\sqrt{14})^{2}

Данное уравнение задает окружность с центром в точке (2;3) и радиусом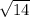 \sqrt{14}, значит симметричная фигура - это окружность с центром в точке (-2; -3) и радиусом

Фактически нужно найти площадь круга. По формуле площади круга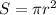 S = \pi r^{2} найдем площади круга, ограниченного данной окружностью:

S = \pi r^{2} = \pi (\sqrt{14} )^{2} = 14\pi

Важно: уравнение окружности с центром в точке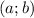 (a; b) и радиусом r задается так:

(x - a)^{2} + (y - b)^{2} = r^{2}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
VadimOMG VadimOMG  17.12.2020 06:50
ответьте «да» или «нет»1) Треугольник равносторонний, то все его стороны равны.2) В равнобедренном треугольнике медиана является высотой и биссектрисой.3) Если боковая...
Goym Goym  17.12.2020 06:49
Определи длину данных векторов, если известны их координаты. (Если это необходимо, ответ округли до десятых.)a→{−12;5}  ∣∣a→∣∣= ; b→{5;−12}  ∣∣∣b→∣∣∣= ; c→{−7;−24}  ∣∣c→∣∣= ; d→{−24;−7}  ∣∣∣d→∣∣∣= .ответить!​...
alisatcheredinp0805h alisatcheredinp0805h  17.12.2020 06:49
Дано:угл 1 равен углу 2 Найти:параллельные прямые​...
alexlol228 alexlol228  17.12.2020 06:47
Точка пересечения O — серединная точка для обоих отрезков AD и RM. Найди величину углов ∡A и ∡R в треугольнике ARO, если ∡M = 47° и ∡D = 32°.​...
alinaetosila2004 alinaetosila2004  17.12.2020 06:45
Отрезок NE - это середина равнобедренного треугольника MNK, проведенная к его основанию, ZMNK - 128 °, ZM - 26 °. Найдите углы треугольника NEK....
busiginanst99 busiginanst99  17.12.2020 06:43
Точка пересечения O — серединная точка для обоих отрезков AD и RM. Найди величину углов ∡A и ∡R в треугольнике ARO, если ∡M = 47° и ∡D = 32°.​...
victory66 victory66  17.12.2020 06:43
Найдите площадь круга, вписанного в правильный треугольник со стороной а​...
Sumiya666 Sumiya666  17.12.2020 06:42
Катеты прямоугольного треугольника равны 7 см и 24 см. Определи длину медианы, проведённую к гипотенузе этого треугольника. Медиана равна см....
Макс332211 Макс332211  17.12.2020 06:39
Точки A и C расположены по одну сторону от прямой, к которой от обеих точек проведены перпендикуляры AB и CD равной длины. Определи величину угла∡ABC, если ∡ADB = 63...
0HIMiK0 0HIMiK0  17.12.2020 06:30
Дано: ABCD — параллелограмм, BC= 2 см, BA= 7 см, ∡ B равен 30°. Найти: площадь треугольника S(ABC) и площадь параллелограмма S(ABCD) SΔABC= см2; S(ABCD)= см2....

Популярные вопросы