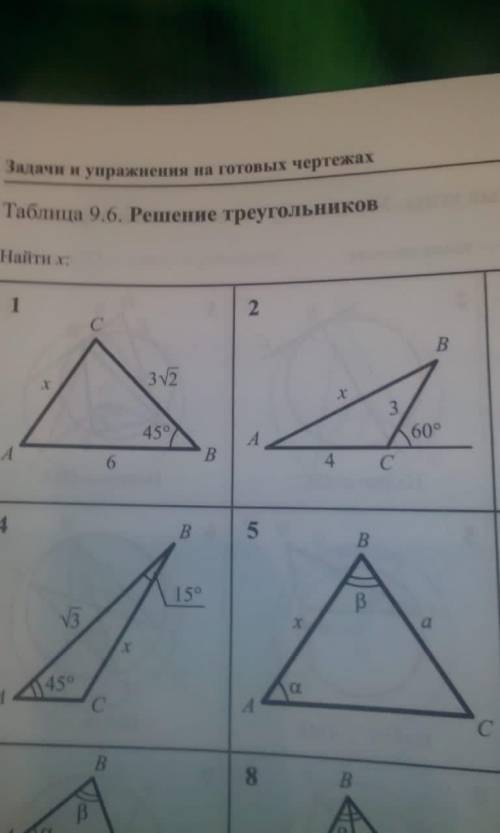
Здравствуйте решить задания по геометри 2,4,5

Здравствуйте! Давайте решим задачи по геометрии 2, 4 и 5.

Задача 2:
На данной картинке мы видим два прямоугольника, один из которых объединен с полукруглой фигурой. Наша задача - найти площадь этой фигуры.

Для начала посмотрим на прямоугольники. Первый прямоугольник имеет ширину 8 см и длину 12 см. Чтобы найти его площадь, нужно умножить эти два числа: 8 см * 12 см = 96 см².

Второй прямоугольник имеет ширину 5 см и длину 10 см. Также умножаем эти числа: 5 см * 10 см = 50 см².

Теперь посмотрим на полукруглую фигуру. Она имеет радиус 7 см. Площадь полукруга вычисляется по формуле: площадь = π * r² / 2, где π - это приближенное значение числа Пи (около 3,14), а r - радиус полукруга.

Подставляем значения в формулу: площадь = 3,14 * 7² / 2 = 3,14 * 49 / 2 ≈ 76,985 см².

Теперь объединяем площади прямоугольников и полукруга: 96 см² + 50 см² + 76,985 см² ≈ 222,985 см².

Ответ: площадь объединенной фигуры примерно равна 222,985 квадратных сантиметров.

Задача 4:
На данной картинке показан прямоугольник со сторонами 20 см и 10 см, а также прямоугольник со сторонами 15 см и 7 см. Задача состоит в том, чтобы найти площадь этой фигуры.

Для начала находим площади прямоугольников. Первый прямоугольник имеет площадь: площадь = 20 см * 10 см = 200 см².
Второй прямоугольник имеет площадь: площадь = 15 см * 7 см = 105 см².

Теперь суммируем эти две площади: 200 см² + 105 см² = 305 см².

Ответ: площадь объединенной фигуры равна 305 квадратным сантиметрам.

Задача 5:
В этой задаче нам нужно найти площадь прямоугольника, на котором отмечены отрезки длиной 8 см и 5 см.

Находим площадь прямоугольника, чтобы найти площадь одной из его частей. У нас есть два отрезка, один из которых длиной 8 см, а другой - 5 см. Мы знаем, что эти отрезки являются сторонами прямоугольника, а площадь прямоугольника находится как произведение его сторон.

Умножаем длины отрезков: 8 см * 5 см = 40 см².

Ответ: площадь прямоугольника, на котором отмечены отрезки длиной 8 см и 5 см, равна 40 квадратным сантиметрам.

Надеюсь, я смог помочь вам понять эти задачи по геометрии. Если у вас остались какие-либо вопросы, не стесняйтесь спрашивать.