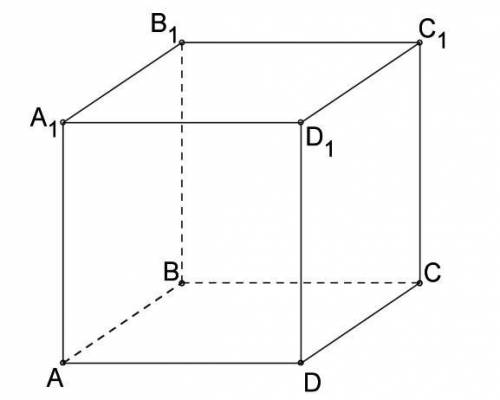
Здравствуйте! Нужна ! Дан куб ABCDA1B1C1D1.
Задание 1.

Выпишите:

а) пару параллельных прямых;

б) пару пересекающихся прямых;

в) пару скрещивающихся прямых;

г) пару параллельных плоскостей.

Задание 2.

Назовите прямую, которая:

а) параллельна плоскости DD1C1;

б) параллельна плоскости A1B1C1 и плоскости BB1C1;

в) является скрещивающейся с прямой AD и пересекает прямую AA1.

Задание 3

Определите угол между прямыми AB и CD1. Выполните построение, обоснуйте ответ.

Задание 4

Середины рёбер AD, BC, CC1, DD1 куба последовательно соединили так, что образовался четырёхугольник. Докажите, что этот четырёхугольник плоский и является параллелограммом.

Здравствуйте! Давайте разберем по порядку каждое задание.

Задание 1:
а) Пара параллельных прямых. В данном случае можно найти несколько пар параллельных прямых. Например, AB и A1B1, BC1 и C1D1. Если мы продолжим эти прямые за границы куба, то они никогда не пересекутся.
б) Пара пересекающихся прямых. Здесь мы можем найти несколько пар пересекающихся прямых. Например, AB и AD1, AB и B1C.
в) Пара скрещивающихся прямых. В этом случае можно выбрать пару CD1 и B1C, CD1 и AD.
г) Пара параллельных плоскостей. Есть несколько пар параллельных плоскостей. Например, ABCC1 и A1B1C1D1, ABCD и C1D1B1A1.

Задание 2:
а) Прямая параллельна плоскости DD1C1. Это означает, что прямая принадлежит этой плоскости или лежит вне нее, но не пересекает ее.
б) Прямая параллельна плоскости A1B1C1 и плоскости BB1C1. То есть прямая находится в одной и той же плоскости со всеми этими прямыми и ни с одной из них не пересекается.
в) Прямая скрещивается с прямой AD и пересекает прямую AA1. Это значит, что эта прямая проходит через прямую AD и пересекает прямую AA1 в некоторой точке.

Задание 3:
Чтобы определить угол между прямыми AB и CD1, нужно построить данные прямые и найти точку их пересечения. Затем, с помощью угломера или другого инструмента измеряем угол между этими прямыми. Результат измерения будет являться углом между прямыми AB и CD1.

Задание 4:
Чтобы доказать, что четырехугольник ABCD является плоским параллелограммом, воспользуемся свойствами геометрических фигур. В данном случае, мы знаем, что середины ребер AD и BC соединены отрезком MN.
1) Докажем, что MN параллельно AB. Для этого можно использовать свойство серединных перпендикуляров. То есть, проводим перпендикуляры из точек A и B к прямой MN. Из-за свойств серединных перпендикуляров, эти перпендикуляры будут пересекаться в точке MN/2 и делиться пополам. Если полученные точки пересечения совпадут, то это будет означать, что MN параллельно AB.
2) Далее, чтобы доказать, что ABCD является параллелограммом, нужно доказать, что AB параллельно CD и AD параллельно BC. Это можно сделать, используя свойства параллельных линий. Если мы докажем, что углы ABM и CMD равны, а также углы AMB и CDM равны, то это будет означать, что AB параллельно CD и AD параллельно BC.
3) Для доказательства плоскости четырехугольника ABCD, можно провести диагонали AC и BD. Если эти диагонали пересекутся в точке O и будут делиться пополам, то это будет означать, что ABCD лежит в одной плоскости.

Вот таким образом мы можем решить данные задания подробно и обоснованно. Я надеюсь, что ответы понятны и помогут вам. Если у вас есть еще вопросы, пожалуйста, обращайтесь!